题目内容
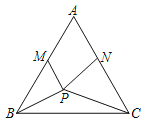
【题目】等边三角形ABC中，∠BPC＝150°，BP＝3，PC＝4，M、N分别为AB，AC上两点，且AM＝AN，则PM+PN的最小值为__．
【答案】5．
【解析】
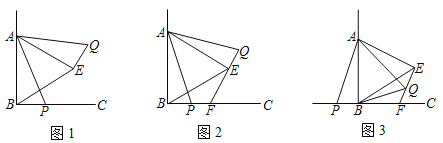
如图1中，将△BCP绕点C顺时针旋转60°得到△ACE．得到△PCE是等边三角形，根据勾股定理得到PA=
=5，如图2中，将△APM绕点A逆时针旋转60°得到△AFN．得到△PAF是等边三角形，PM=NF，于是得到结论．
如图1中，将△BCP绕点C顺时针旋转60°得到△ACE．
则△PCE是等边三角形，∠AEC＝∠BPC＝150°，∠PEC＝60°，
∴∠AEP＝90°，
∵AE＝BP＝3，PC＝PE＝4，
∴PA＝＝5，
如图2中，如图1中，将△APM绕点A逆时针旋转60°得到△AFN．
则△PAF是等边三角形，PM＝NF，
∴PF＝AP＝5，
∵PM+PN＝NF+NP≥PF，
∴PM+PN≥5，
∴PM+PN的最小值为5，
故答案为：5．
练习册系列答案
相关题目
【题目】某甜品店计划订购一种鲜奶，根据以往的销售经验，当天的需求量与当天的最高气温T有关，现将去年六月份（按30天计算）的有关情况统计如下：（最高气温与需求量统计表）
最高气温（单位：摄氏度） | 需求量（单位：杯） |
T<25 | 250 |
| 300 |
| 400 |
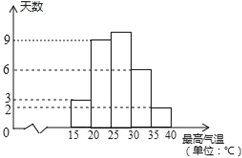
（1）求去年六月份最高气温不高于30℃的天数．
（2）若以最高气温位于各区间的频率估计最高气温位于该区间的概率，求去年六月份这种鲜奶一天的需求量不超过250杯的概率．
（3）若今年六月份每天的进货量均为350杯，每杯的进价为5元，售价为10元，未售出的这种鲜奶厂家以1元的价格收回销毁，假设今年与去年的情况大致一样，若今年六月份某天的最高气温T满足大于等于25℃小于30℃ ，试估计这一天销售这种鲜奶所获得的利润为多少元？
