题目内容
| |||||||||||||||
解析:
(1) |
解:(1) 过点O作EF∥AD,分别交AB、CD于点E、F 则 ∴OE= ∴OF=EF–OE=4– 在Rt△APB中 ∴PB= ∴OP= ∵ ∴OF>OP ∴CD与⊙O相离 |
(2) |
设BC与⊙O交于点M,连结PM,在△ABP和△MPB中 ∵ ∴△ABP≌△MPB ∴AP=MB 设MB=AP=x(x>0) 则OE = OF=EF–OE = 4– PB= OP= ∵CD与⊙O相切 ∴OF=OP ∴4– 解得 x= ∴BC被⊙O截得的弦长为 |
(3) |
∵点P在⊙O上 ∴CP只可能与⊙O相切或相交 令PC与⊙O相切于点P,连结PC,则∠CPB=∠BAP=90° 由∠5+∠6 = 90°,∠7+∠6=90 ∴∠5=∠7 ∴△ABP∽△PCB ∴ 设AP=x(x>0) ∴BP= ∴x2+9=ax即x2-ax+9=0 ∴方程x2-ax+9=0有正实数解,设方程x2-ax+9=0的两实数根分别为x1、x2 又∵ ∴△= a2-4×1×9=a2-36 令y=a2-36,观察其函数图象,考虑到 a>0,得 当a≥6时,△≥0 ∴当0<a<6时,CP不可能与⊙O相切,无论点P是边AD上任一点(除端点A外),CP都与⊙O相交 |

 名校课堂系列答案
名校课堂系列答案







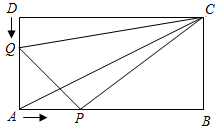 如下图,在矩形ABCD中,AB=12cm,BC=6cm.点P沿AB边从点A开始向点B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1 cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6)那么:
如下图,在矩形ABCD中,AB=12cm,BC=6cm.点P沿AB边从点A开始向点B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1 cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6)那么:


