题目内容
 如图,在⊙O中,直径AB⊥弦CD于E,连接BD,若∠D=30°,BD=2,则AE的长为
如图,在⊙O中,直径AB⊥弦CD于E,连接BD,若∠D=30°,BD=2,则AE的长为
- A.2
- B.3
- C.4
- D.5
B
分析:先根据直角三角形的性质求出BE及DE的长,再连接OD,设OD=r,则OE=r-BE,在Rt△ODE中利用勾股定理求出r的值,进而可得出AE的长.
解答: 解:∵AB⊥CD,∠D=30°,BD=2,
解:∵AB⊥CD,∠D=30°,BD=2,
∴△BDE是直角三角形,
∴BE= BD=
BD= ×2=1,
×2=1,
∴DE=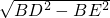 =
= =
= ,
,
连接OD,设OD=r,则OE=r-BE=r-1,
在Rt△ODE中,
OD2=OE2+DE2,即r2=(r-1)2+( )2,解得r=2,
)2,解得r=2,
∴AE=OA+OE=2+(2-1)=3.
故选B.
点评:本题考查的是圆周角定理及勾股定理、直角三角形的性质,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
分析:先根据直角三角形的性质求出BE及DE的长,再连接OD,设OD=r,则OE=r-BE,在Rt△ODE中利用勾股定理求出r的值,进而可得出AE的长.
解答:
 解:∵AB⊥CD,∠D=30°,BD=2,
解:∵AB⊥CD,∠D=30°,BD=2,∴△BDE是直角三角形,
∴BE=
 BD=
BD= ×2=1,
×2=1,∴DE=
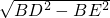 =
= =
= ,
,连接OD,设OD=r,则OE=r-BE=r-1,
在Rt△ODE中,
OD2=OE2+DE2,即r2=(r-1)2+(
 )2,解得r=2,
)2,解得r=2,∴AE=OA+OE=2+(2-1)=3.
故选B.
点评:本题考查的是圆周角定理及勾股定理、直角三角形的性质,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
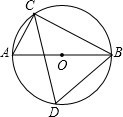 如图,在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,则BC=
如图,在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,则BC=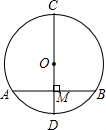 如图,在⊙O中,直径CD的长度为10cm,AB是弦,且AB⊥CD于M,OM=3cm,求弦AB的长.
如图,在⊙O中,直径CD的长度为10cm,AB是弦,且AB⊥CD于M,OM=3cm,求弦AB的长.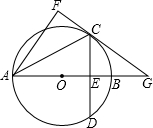 C与直线AB相交于点G.
C与直线AB相交于点G. (2013•百色)如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是( )
(2013•百色)如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是( ) (2012•朝阳区二模)如图,在⊙O中,直径AB⊥弦CD于点H,E是⊙O上的点,若∠BEC=25°,则∠BAD的度数为( )
(2012•朝阳区二模)如图,在⊙O中,直径AB⊥弦CD于点H,E是⊙O上的点,若∠BEC=25°,则∠BAD的度数为( )