Question

【题目】综合与实践

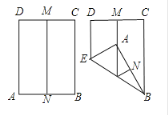
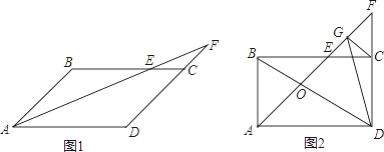
（1）实践操作：中，，为直线上一点，过点作，与直线相交于点，如图①，图②，图③所示，则的形状为______.

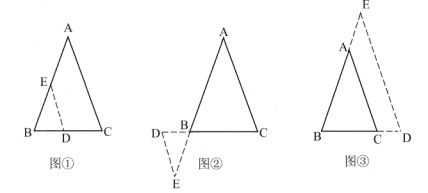
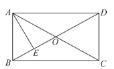
（2）问题解决：等腰三角形是一种特殊的三角形，常与全等三角形的相关知识结合在一起解决问题.如图④，中，，为上一点，为延长线上一点，且，交于，求证：.

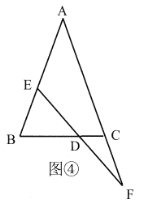
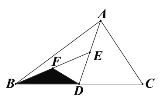
（3）拓展与应用,在（2）的条件下，如图⑤，过点作的垂线，垂足为，若，则的长为______.

Answer 1

【答案】（1）等腰三角形；（2）见解析；（3）3

【解析】

（1）根据平行线的性质证得角相等再进行判断即可；

（2）过点E作交BC于点G，先根据平行线的性质证得，，再根据等腰三角形性质得出EG=FC，然后证的，最后根据全等三角形的性质即可证明；

（3）过点E作交BC于点G，根据（2）中可得，再根据等腰三角形性质得即可求解.

（1）∵

∴

在图①中：

∵

∴

∴

∴

∴为等腰三角形；

在图②中：

∵

∴

∵

∴

∴为等腰三角形；

在图③中：

∵

∴

∴

∴

∴为等腰三角形；

（2）过点E作交BC于点G，如图④-1所示：

∵

∴，

∴

∴

∵

∴

又∵

∴

∴

（3）过点E作交BC于点G，如图⑤-1所示：

由（2）中可得

∵，且

∴

∴