题目内容
(2012•台州)请你规定一种适合任意非零实数a,b的新运算“a⊕b”,使得下列算式成立:
1⊕2=2⊕1=3,(-3)⊕(-4)=(-4)⊕(-3)=-
,(-3)⊕5=5⊕(-3)=-
,…
你规定的新运算a⊕b=
(用a,b的一个代数式表示).
1⊕2=2⊕1=3,(-3)⊕(-4)=(-4)⊕(-3)=-
| 7 |
| 6 |
| 4 |
| 15 |
你规定的新运算a⊕b=
| 2a+2b |
| ab |
| 2a+2b |
| ab |
分析:由题中的新定义,将已知的等式结果变形后,总结出一般性的规律,即可用a与b表示出新运算a⊕b.
解答:解:根据题意可得:
1⊕2=2⊕1=3=
+
,
(-3)⊕(-4)=(-4)⊕(-3)=-
=
+
,
(-3)⊕5=5⊕(-3)=-
=
+
,
则a⊕b=
+
=
.
故答案为:
.
1⊕2=2⊕1=3=
| 2 |
| 1 |
| 2 |
| 2 |
(-3)⊕(-4)=(-4)⊕(-3)=-
| 7 |
| 6 |
| 2 |
| -3 |
| 2 |
| -4 |
(-3)⊕5=5⊕(-3)=-
| 4 |
| 15 |
| 2 |
| -3 |
| 2 |
| 5 |
则a⊕b=
| 2 |
| a |
| 2 |
| b |
| 2a+2b |
| ab |
故答案为:
| 2a+2b |
| ab |
点评:此题考查了有理数的混合运算,属于新定义的题型,其中弄清题意,找出一般性的规律是解本题得关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



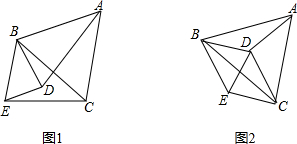 意一点,∠ABC=∠DBE,BD=BE.
意一点,∠ABC=∠DBE,BD=BE.