题目内容
 如图,AB是圆O的直径,弦CD⊥AB于E,P是BA延长线上一点,连接PC交圆O于F,若PF=7,FC=13,PA:AE:EB=2:4:1,则CD长为
如图,AB是圆O的直径,弦CD⊥AB于E,P是BA延长线上一点,连接PC交圆O于F,若PF=7,FC=13,PA:AE:EB=2:4:1,则CD长为分析:本题可先设BE为x,根据割线定理求得x的值,进一步根据相交弦定理的推论求得CE的长,最后再根据垂径定理求得CD的长.
解答:解:设BE为x,则PA=2x,PB=7x.
根据割线定理,得
PA•PB=PF•PC,
即2x•7x=7×20,
解得x=
.
又CE2=AE•BE=4x2=40,
∴CE=2
,
∴CD=2CE=4
.
根据割线定理,得
PA•PB=PF•PC,
即2x•7x=7×20,
解得x=
| 10 |
又CE2=AE•BE=4x2=40,
∴CE=2
| 10 |
∴CD=2CE=4
| 10 |
点评:此题综合运用了割线定理和相交弦定理及其推论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 四边形是平行四边形.
四边形是平行四边形. x+2与y轴的交点A和点M(-
x+2与y轴的交点A和点M(- ,0).
,0).
 x+2与y轴的交点A和点M(-
x+2与y轴的交点A和点M(- ,0).
,0).
 x+2与y轴的交点A和点M(-
x+2与y轴的交点A和点M(- ,0).
,0).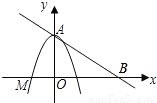
 x+2与y轴的交点A和点M(-
x+2与y轴的交点A和点M(- ,0).
,0).