题目内容
 如图,在长方形ABCD中,AB=2cm,BC=3cm,E、F分别是AD、BC的中点,如果将长方形ABFE绕点F顺时针旋转90°,则旋转后的长方形与长方形CDEF重叠部分的面积是( )cm2.
如图,在长方形ABCD中,AB=2cm,BC=3cm,E、F分别是AD、BC的中点,如果将长方形ABFE绕点F顺时针旋转90°,则旋转后的长方形与长方形CDEF重叠部分的面积是( )cm2.分析:将长方形ABFE绕点F顺时针旋转90度,旋转后的长方形与长方形CDEF重叠部分是一个正方形,其边长为FC=1.5cm,根据正方形的面积公式即可求解.
解答: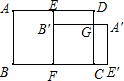 解:如图,将长方形ABFE绕点F顺时针旋转90度,得到长方形A′B′FE′,设A′B′与DC交于点G,
解:如图,将长方形ABFE绕点F顺时针旋转90度,得到长方形A′B′FE′,设A′B′与DC交于点G,
则FC=FB=FB′=
BC=1.5cm,
所以旋转后的长方形A′B′FE′与长方形CDEF重叠部分B′FCG是正方形,边长为1.5cm,
所以,面积S=1.5×1.5=2.25(cm2).
故选B.
 解:如图,将长方形ABFE绕点F顺时针旋转90度,得到长方形A′B′FE′,设A′B′与DC交于点G,
解:如图,将长方形ABFE绕点F顺时针旋转90度,得到长方形A′B′FE′,设A′B′与DC交于点G,则FC=FB=FB′=
| 1 |
| 2 |
所以旋转后的长方形A′B′FE′与长方形CDEF重叠部分B′FCG是正方形,边长为1.5cm,
所以,面积S=1.5×1.5=2.25(cm2).
故选B.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等,也考查了矩形、正方形的性质.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
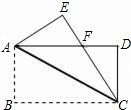 于点F.
于点F. 如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.
如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.

