题目内容
数轴上表示1、| 2 |
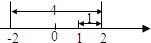
分析:先结合数轴求出AB之间的距离,然后根据对称的性质得出CA之间的距离,再求出OC之间的距离即可求解.
解答:解:∵数轴上表示1、
的对应点分别为A、B,
∴|AB|=
-1,
∵点B和点C关于点A对称,
∴|AC|=
-1,
∴|OC|=1-(
-1)=2-
,
∴C点表示的数是2-
.
| 2 |
∴|AB|=
| 2 |
∵点B和点C关于点A对称,
∴|AC|=
| 2 |
∴|OC|=1-(
| 2 |
| 2 |
∴C点表示的数是2-
| 2 |
点评:本题考查了实数与数轴上的点的对应关系,以及对称的有关性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,数轴上表示1,
如图,数轴上表示1,| 2 |
A、1-
| ||
B、2-
| ||
C、
| ||
D、
|
操作与思考
探索性问题:
已知点A,B在数轴上的位置所表示的数分别用![]() 表示.利用数形结合思想回答下列问题:
表示.利用数形结合思想回答下列问题:
(1)填写下表:
| 数 | 第1组 | 第2组 | 第3组 | 第4组 | 第5组 | 第6组 | … |
|
| 5 | -5 | 6 | -6 | -10 | -2.5 | … |
|
| 3 | 0 | -4 | -4 | 2 | -2.5 | … |
| A,B两点的距离 | 2 | 0 | … |
(2)通过对上表中具体数据的研究和归纳,你发现数轴上表示![]() 和
和![]()
![]() 两点之间的距离表示为 .
两点之间的距离表示为 .
(3)若![]() 表示一个有理数,则
表示一个有理数,则![]() 的最小值是 .
的最小值是 .
 28、
28、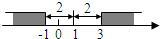 阅读下列材料:
阅读下列材料: