题目内容
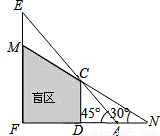
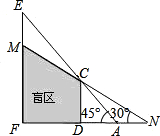如图所示，CD、EF表示高度不同的两座建筑物，已知CD高15米，小明站在A处，视线越过CD，能看到它后面的建筑物的顶端E，此时小明的视角∠FAE=45°，为了能看到建筑物EF上点M的位置，小明延直线FA由点A移动到点N的位置，此时小明的视角∠FNM=30°，则小明由点A移动到点N的距离是________米．
15
分析：本题中，CD是直角三角形CDN和ACD的公共边，因此可用CD求出DN和AD，然后再求AN．
解答：直角三角形CDN中，DN=CD÷tan30°=15
米，
直角三角形CDA中，AD=CD÷tan45°=15米，
因此，AN=DN-AD=（15-15）米．
点评：利用数学知识解决实际问题是中学数学的重要内容．解决此问题的关键在于正确理解题意的基础上建立数学模型，把实际问题转化为数学问题．
分析：本题中，CD是直角三角形CDN和ACD的公共边，因此可用CD求出DN和AD，然后再求AN．
解答：直角三角形CDN中，DN=CD÷tan30°=15
米，直角三角形CDA中，AD=CD÷tan45°=15米，
因此，AN=DN-AD=（15
-15）米．点评：利用数学知识解决实际问题是中学数学的重要内容．解决此问题的关键在于正确理解题意的基础上建立数学模型，把实际问题转化为数学问题．
练习册系列答案
相关题目
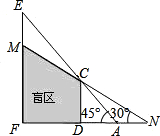如图所示，CD、EF表示高度不同的两座建筑物，已知CD高15米，小明站在A处，视线越过CD，能看到它后面的建筑物的顶端E，此时小明的视角∠FAE=45°，为了能看到建筑物EF上点M的位置，小明延直线FA由点A移动到点N的位置，此时小明的视角∠FNM=30°，则小明由点A移动到点N的距离是
