题目内容
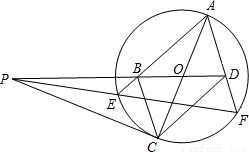
如图,PC切圆O于C,AC为圆的直径,PEF为圆的割线,AE、AF与直线PO相交于B、D.求证:AB=DC,BC=AD.

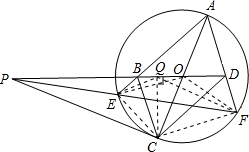
证明:作CQ⊥PD于Q,连接EO,EQ,EC,OF,QF,CF,
所以PC2=PQ?PO(射影定理),
又PC2=PE?PF,
所以EFOQ四点共圆,
∠EQF=∠EOF=2∠BAD,
又∠PQE=∠OFE=∠OEF=∠OQF,
而CQ⊥PD,所以∠EQC=∠FQC,因为∠AEC=∠PQC=90°,
故B、E、C、Q四点共圆,
所以∠EBC=∠EQC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CB∥AD,
所以BO=DO,即四边形ABCD是平行四边形,
∴AB=DC,BC=AD.

练习册系列答案
相关题目
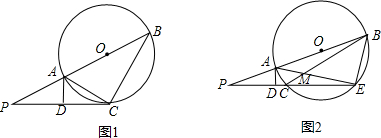 点,AE与BC交于点M,AD⊥PE,写出图2中相等的角(写出三组即可,直角除外);
点,AE与BC交于点M,AD⊥PE,写出图2中相等的角(写出三组即可,直角除外);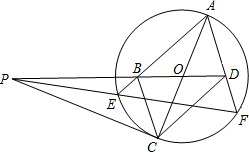 如图,PC切圆O于C,AC为圆的直径,PEF为圆的割线,AE、AF与直线PO相交于B、D.求证:AB=DC,BC=AD.
如图,PC切圆O于C,AC为圆的直径,PEF为圆的割线,AE、AF与直线PO相交于B、D.求证:AB=DC,BC=AD. 如图,PC切圆O于C,AC为圆的直径,PEF为圆的割线,AE、AF与直线PO相交于B、D.求证:AB=DC,BC=AD.
如图,PC切圆O于C,AC为圆的直径,PEF为圆的割线,AE、AF与直线PO相交于B、D.求证:AB=DC,BC=AD.