题目内容
已知两个全等的直角三角形纸片ABC、DEF,如图⑴放置,点B、D重合,点F在BC上,AB与EF交于点G.∠C=∠EFB=90°,∠E=∠ABC=30°,AB=DE=4.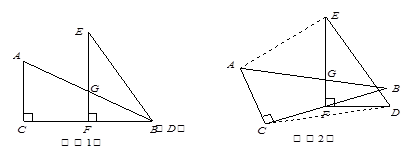
【小题1】求证:△EGB是等腰三角形;
【小题2】若纸片DEF不动,问△ABC绕点F逆时针旋转最小 度时,四边形ACDE成为以ED为底的梯形(如图⑵).求此梯形的高
【小题1】∵∠EFB=90°,∠ABC=30° ∴∠EBG=30°
∵∠E=30° ∴∠E=∠EBG ∴EG=BG
∴△EGB是等腰三角形
【小题1】30°
在Rt△ABC 中,∠C=90°,∠ABC=30°,AB=4 ∴BC= ;
;
在Rt△DEF 中,∠EFD=90°,∠E=30°,DE=4
∴DF=2 ∴CF=
∵四边形ACDE成为以ED为底的梯形 ∴ED∥AC
∵∠ACB=90° ∴ED⊥CB
∵DE=4∴DF=2 ∴F到ED的距离为
∴梯形的高为
解析

练习册系列答案
相关题目
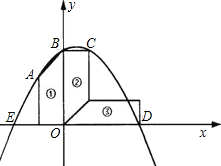 x2-bx-c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6.
x2-bx-c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6.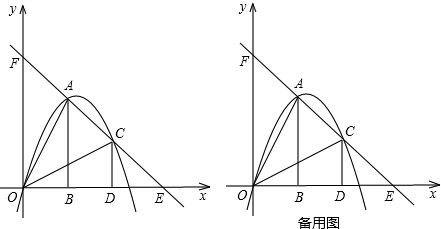
 x2-bx-c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6.
x2-bx-c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6.
