题目内容
22、几何题
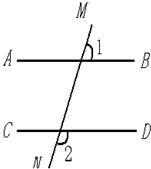
①.如图所示,直线AB∥CD,∠1=75°,求∠2的度数.
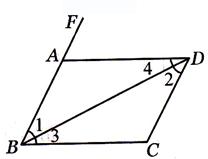
②.如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证DF∥AC.

③.如图,(1)∵AD∥BC
∴∠FAD=
∵∠1=∠2
∴
①.如图所示,直线AB∥CD,∠1=75°,求∠2的度数.

②.如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证DF∥AC.

③.如图,(1)∵AD∥BC
∴∠FAD=
∠ABC
.(两直线平行,同位角相等)
∵∠1=∠2
∴
AB
∥CD
.
分析:(1)由直线AB∥CD,根据两直线平行,同位角相等得到∠1=∠3=75°,利用平角的定义有∠3+∠2=180°,即可计算出∠2的度数.
(2)由∠1=∠2,∠2=∠3,得到∠3=∠1,根据同位角相等,两直线平行得到DB∥EC,再根据两直线平行,内错角相等得到∠C=∠DBA,而∠C=∠D,则∠D=∠DBA,
然后根据平行的判定即可得到结论;
(3)分别根据平行线的性质与判定即可得到答案.
(2)由∠1=∠2,∠2=∠3,得到∠3=∠1,根据同位角相等,两直线平行得到DB∥EC,再根据两直线平行,内错角相等得到∠C=∠DBA,而∠C=∠D,则∠D=∠DBA,
然后根据平行的判定即可得到结论;
(3)分别根据平行线的性质与判定即可得到答案.
解答:(1) 解:
解:
∵直线AB∥CD,
∴∠1=∠3=75°,
而∠3+∠2=180°,
∴∠2=105°;
(2)证明:∵∠1=∠2,
而∠2=∠3,
∴∠3=∠1,
∴DB∥EC,
∴∠C=∠DBA,
而∠C=∠D,
∴∠D=∠DBA,
∴DF∥AC.
(3)∠ABC,(两直线平行,同位角相等);AB,CD.
 解:
解:∵直线AB∥CD,
∴∠1=∠3=75°,
而∠3+∠2=180°,
∴∠2=105°;
(2)证明:∵∠1=∠2,
而∠2=∠3,
∴∠3=∠1,
∴DB∥EC,
∴∠C=∠DBA,
而∠C=∠D,
∴∠D=∠DBA,
∴DF∥AC.
(3)∠ABC,(两直线平行,同位角相等);AB,CD.
点评:本题考查了直线平行的判定与性质:同位角相等,两直线平行;内错角相等,两直线平行;两直线平行,同位角相等;两直线平行,内错角相等.

练习册系列答案
相关题目
 几何计算题:
几何计算题:
 12、如图所示的积木是由16块棱长为acm的正方体堆积而成的.则这个几何题的表面积是
12、如图所示的积木是由16块棱长为acm的正方体堆积而成的.则这个几何题的表面积是 几何计算题:
几何计算题: