题目内容
如图，平行于x轴的直线AC分别交抛物线y1=x2（x≥0）与y2=
（x≥0）于B、C两点，过点C作y轴的平行线交y1于点D，直线DE∥AC，交y2于点E，则
=________．
3-
分析：设A点坐标为（0，a），利用两个函数解析式求出点B、C的坐标，然后求出AB的长度，再根据CD∥y轴，利用y1的解析式求出D点的坐标，然后利用y2求出点E的坐标，从而得到DE的长度，然后求出比值即可得解．
解答：设设A点坐标为（0，a），（a＞0），
则x2=a，解得x=
，
∴点B（，a），
=a，
则x=
，
∴点C（，a），
∵CD∥y轴，
∴点D的横坐标与点C的横坐标相同，为，
∴y1=2=3a，
∴点D的坐标为（，3a），
∵DE∥AC，
∴点E的纵坐标为3a，
∴=3a，
∴x=3，
∴点E的坐标为（3，），
∴DE=3-，
=
=3-．
故答案为：3-．
点评：本题是二次函数综合题型，主要利用了二次函数图象上点的坐标特征，根据平行与x轴的点的纵坐标相同，平行于y轴的点的横坐标相同，求出用点A的纵坐标表示出各点的坐标是解题的关键．
分析：设A点坐标为（0，a），利用两个函数解析式求出点B、C的坐标，然后求出AB的长度，再根据CD∥y轴，利用y1的解析式求出D点的坐标，然后利用y2求出点E的坐标，从而得到DE的长度，然后求出比值即可得解．
解答：设设A点坐标为（0，a），（a＞0），
则x2=a，解得x=
，∴点B（
，a），=a，则x=
，∴点C（
，a），∵CD∥y轴，
∴点D的横坐标与点C的横坐标相同，为
，∴y1=
2=3a，∴点D的坐标为（
，3a），∵DE∥AC，
∴点E的纵坐标为3a，
∴
=3a，∴x=3
，∴点E的坐标为（3
，），∴DE=3
-，==3-．故答案为：3-
．点评：本题是二次函数综合题型，主要利用了二次函数图象上点的坐标特征，根据平行与x轴的点的纵坐标相同，平行于y轴的点的横坐标相同，求出用点A的纵坐标表示出各点的坐标是解题的关键．
练习册系列答案
相关题目
相交于点C．
与x轴交于点A（—2，0），交y轴于点B（0，
）.直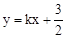
过点A与y轴交于点C，与抛物线的另一个交点是D.
