Question

【题目】在平面直角坐标系中，直线y＝x﹣2与x轴交于点B，与y轴交于点C，二次函数y＝x2+bx+c的图象经过B，C两点，且与x轴的负半轴交于点A．

（1）求二次函数的解析式；

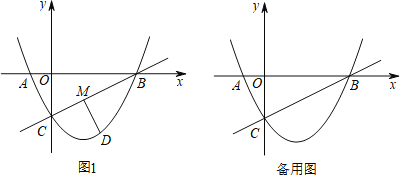
（2）如图1，点M是线段BC上的一动点，动点D在直线BC下方的二次函数图象上．设点D的横坐标为m．

①过点D作DM⊥BC于点M，求线段DM关于m的函数关系式，并求线段DM的最大值；

②若△CDM为等腰直角三角形，直接写出点M的坐标．

Answer 1

【答案】（1）y＝x2﹣x﹣2；（2）①DM＝﹣，DM的最大值为；②M的坐标为（）或（，﹣）．

【解析】

（1）由直线y＝x﹣2得B（4，0）、C（0，﹣2），将B（4，0）、C（0，﹣2）代入y＝x2+bx+c，列方程组求出b、c即可；

（2）①过点DH∥AB，交直线y＝x﹣2于点H．则∠H＝∠OBC，OC＝2，OB＝4，BC＝2，由sin∠H＝sin∠OBC＝＝＝，即＝，设D（m，m2﹣m﹣2），则H（m2﹣3m，m2﹣m﹣2），DH＝m﹣（m2﹣3m）＝﹣m2+4m，所以DM＝（﹣m2+4m）＝﹣，当m＝2时，DM的最大值为；

②分两种情况：当CM⊥DM时，过点M作ME⊥y轴于点E，点D作DF∥y轴，交EM的延长线于点F；当CD⊥DM时，过点D作DE⊥y轴于点E，点M作MF∥y轴，交ED的延长线于点F，分别求出t的值即可．

解（1）由直线y＝x﹣2得

B（4，0）、C（0，﹣2），

将B（4，0）、C（0，﹣2）代入y＝x2+bx+c，

，

解得b＝，c＝﹣2，

∴二次函数的解析式y＝x2﹣x﹣2；

（2）①过点DH∥AB，交直线y＝x﹣2于点H．

∴∠H＝∠OBC，

∵B（4，0）、C（0，﹣2），

∴OC＝2，OB＝4，BC＝2

∴sin∠H＝sin∠OBC＝＝＝，

即＝，

设D（m，m2﹣m﹣2），则H（m2﹣3m，m2﹣m﹣2），

∴DH＝m﹣（m2﹣3m）＝﹣m2+4m，

∴DM＝（﹣m2+4m）＝﹣，

当m＝2时，DM的最大值为；

②Ⅰ．当CM⊥DM时，过点M作ME⊥y轴于点E，点D作DF∥y轴，交EM的延长线于点F，

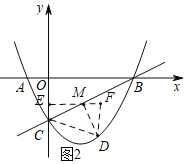
∵△CDM为等腰直角三角形，易证△EMC≌△FDM，

∴EM＝DF，EC＝MF，

设M（t，t﹣2），则EM＝t，OE＝﹣t+2，

∴CE＝OC﹣OE＝2﹣（﹣t+2）＝t，MF＝t，DF＝t，

EF＝EM+MF＝t+t＝，OE+DF＝﹣t+2+t＝t+2，

∴D（t，﹣t﹣2）

将D（t，﹣t﹣2）代入二次函数的解析式y＝x2﹣x﹣2，

，

解得t＝0（舍去）或t＝，

∴M1（）；

Ⅱ．当CD⊥DM时，过点D作DE⊥y轴于点E，点M作MF∥y轴，交ED的延长线于点F，

∵△CDM为等腰直角三角形，易证△CED≌△DFM，

∴DE＝MF，EC＝DF，

设M（t，t﹣2），则EF＝t，CE＝，DE＝t，MF＝t，OC＝t+2

∴D（t，﹣t﹣2），

将D（t，﹣t﹣2）代入二次函数的解析式y＝x2﹣x﹣2，

，

解得t＝0（舍去）或t＝，

∴M2（，﹣）

综上，△CDM为等腰直角三角形，点M的坐标为（）或（，﹣）．