题目内容
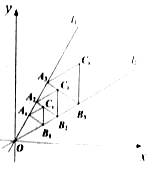
【题目】如图,点![]() 在直线
在直线![]() 上,过点
上,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,
,![]() 为边在
为边在![]() 外侧作等边三角形
外侧作等边三角形![]() ,再过点
,再过点![]() 作
作![]() ,分别交直线
,分别交直线![]() 和
和![]() 于
于![]() 两点,以
两点,以![]() 为边在
为边在![]() 外侧作等边三角形
外侧作等边三角形![]() 按此规律进行下去,则第
按此规律进行下去,则第![]() 个等边三角形
个等边三角形![]() 的面积为__________.(用含
的面积为__________.(用含![]() 的代数式表示)
的代数式表示)
【答案】![]() .
.
【解析】
试题分析:由点A1的坐标可得出OA1=2,根据直线l1、l2的解析式结合解直角三角形可求出A1B1的长度,由等边三角形的性质可得出A1A2的长度,进而得出OA2=3,通过解直角三角形可得出A2B2的长度,同理可求出AnBn的长度,再根据等边三角形的面积公式即可求出第n个等边三角形AnBnCn的面积.
∵点A1(1,![]() ),∴OA1=2.
),∴OA1=2.
∵直线l1:y=![]() x,直线l2:y=
x,直线l2:y=![]() x,∴∠A1OB1=30°.
x,∴∠A1OB1=30°.
在Rt△OA1B1中,OA1=2,∠A1OB1=30°,∠OA1B1=90°,
∴A1B1=![]() OB1,∴A1B1=
OB1,∴A1B1=![]() .
.
∵△A1B1C1为等边三角形,∴A1A2=![]() A1B1=1,
A1B1=1,
∴OA2=3,A2B2=![]() .
.
同理,可得出:A3B3=![]() ,A4B4=
,A4B4=![]() ,…,AnBn=
,…,AnBn=![]() ,
,
∴第n个等边三角形AnBnCn的面积为![]() .
.
故答案为:![]() .
.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目