题目内容
 (1)在图1中,求作△ABC的外接圆(尺规作图,不写作法保留痕迹);
(1)在图1中,求作△ABC的外接圆(尺规作图,不写作法保留痕迹);
(2)如图2,若△ABC的内心为O,且BA=BC=8,sinA= ,求△ABC的内切圆半径.
,求△ABC的内切圆半径.
 解:(1)如图所示:
解:(1)如图所示:(2)连结BO并延长交AC于F,
∵AB=BC=8,O为△ABC内心,
∴BF⊥AC,AF=CF,
又∵sinA=
 ,
,∴BF=AB sinA=8×
 =6,
=6,∴AF=
 ,
,∴Rt△OBE中:
 ,
,解得半径为:
 ,
,解法二:△面积法:AC=
 ,
,设内接圆半径为R,
 R(AB+AC+BC)=
R(AB+AC+BC)= AC•BF,
AC•BF,解得内接圆半径R=
 .
.分析:(1)首先做出AB,BC的垂直平分线,进而得出圆心位置,进而利用圆心到顶点距离为半径,即可得出外接圆;
(2)首先连结BO并延长交AC于F,得出BF⊥AC,进而得出BF,AF的长,求出半径即可.
点评:此题主要考查了复杂作图以及三角形内切圆的作法和锐角三角函数的应用等知识,根据已知得出AF的长进而利用勾股定理求出是解题关键.

练习册系列答案
相关题目
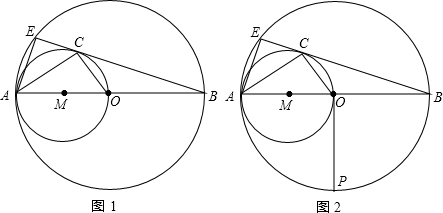
 (2013•拱墅区一模)(1)在图1中,求作△ABC的外接圆(尺规作图,不写作法保留痕迹);
(2013•拱墅区一模)(1)在图1中,求作△ABC的外接圆(尺规作图,不写作法保留痕迹);
 ,求△ABC的内切圆半径.
,求△ABC的内切圆半径.