题目内容
(2007•宜宾)已知:如图,在半径为4的⊙O中,圆心角∠AOB=90°,以半径OA、OB的中点C、F为顶点作矩形CDEF,顶点D、E在⊙O的劣弧 上,OM⊥DE于点M.试求图中阴影部分的面积.(结果保留π)
上,OM⊥DE于点M.试求图中阴影部分的面积.(结果保留π)
【答案】分析:由图知,阴影部分的面积等于扇形OAB的面积减去等腰直角三角形OAB的面积再减去矩形PQED的面积.求得相关的线段后即可得解.
解答: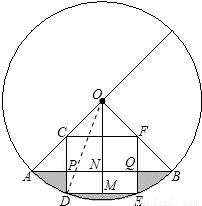 解:∵∠AOB=90°,
解:∵∠AOB=90°,
∴扇形AOB的面积=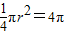 .(1分)
.(1分)
∵C、F分别为OA、OB的中点,OA=OB=4,
∴OC=OF=2,CF=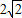 .(2分)
.(2分)
∴CF平行且等于 AB.
AB.
∴AB=2CF=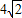 .(3分)
.(3分)
∴CF∥AB∥DE,
∴CD⊥AB,FE⊥AB.
∵OM⊥DE,
∴OM⊥AB.
∵△AON为等腰直角三角形,且OA=4,
∴ON=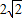 .连接OD,
.连接OD,
∵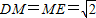 ,
,
∴ .
.
∴MN=PD=QE=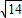 -
-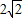 .(4分)
.(4分)
∴矩形PDEQ的面积=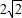 ×(
×(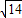 -
-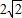 )=
)=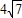 -8.(5分)
-8.(5分)
∴S阴影=S扇形AOB-S△AOB-S矩形PDEQ
=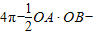 (
(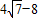 )
)
=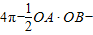 (
(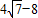 )
)
=4π-8-(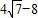 )
)
=4π- .(6分)
.(6分)
点评:本题关键是求矩形QDEQ的长PQ和宽QE,要利用到等腰直角三角形的性质,矩形的性质,三角形中位线的性质.
解答:
 解:∵∠AOB=90°,
解:∵∠AOB=90°,∴扇形AOB的面积=
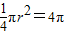 .(1分)
.(1分)∵C、F分别为OA、OB的中点,OA=OB=4,
∴OC=OF=2,CF=
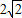 .(2分)
.(2分)∴CF平行且等于
 AB.
AB.∴AB=2CF=
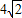 .(3分)
.(3分)∴CF∥AB∥DE,
∴CD⊥AB,FE⊥AB.
∵OM⊥DE,
∴OM⊥AB.
∵△AON为等腰直角三角形,且OA=4,
∴ON=
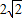 .连接OD,
.连接OD,∵
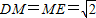 ,
,∴
 .
.∴MN=PD=QE=
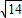 -
-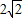 .(4分)
.(4分)∴矩形PDEQ的面积=
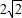 ×(
×(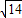 -
-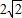 )=
)=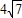 -8.(5分)
-8.(5分)∴S阴影=S扇形AOB-S△AOB-S矩形PDEQ
=
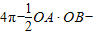 (
(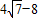 )
)=
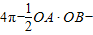 (
(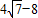 )
)=4π-8-(
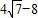 )
)=4π-
 .(6分)
.(6分)点评:本题关键是求矩形QDEQ的长PQ和宽QE,要利用到等腰直角三角形的性质,矩形的性质,三角形中位线的性质.

练习册系列答案
相关题目

 x+3的图象与x轴和y轴交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
x+3的图象与x轴和y轴交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.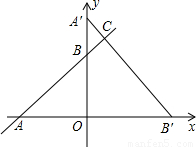

 x+3的图象与x轴和y轴交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
x+3的图象与x轴和y轴交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.