Question

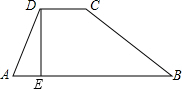
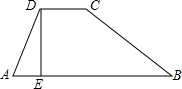
如图是一个水坝的横断面，坝顶宽CD=3O米，坝高DE=4米，迎水坡BC的坡度i₁=1：2，背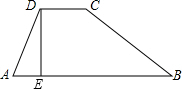水坡的坡度i₂=1：1．
①求角A的度数；
②求坝底的宽AB．

Answer 1

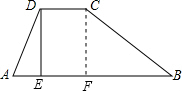解：过点C作CF⊥AB于F．
（1）因为tanA==1：1，即AE=DE，AE⊥DE，
∴∠A=45°；

（2）∵DE⊥AE，DC∥AB，
∴四边形EFCD为矩形，
∴DE=CF=4米，CD=EF=30米，
∵tanB==，
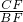∴BF=2CF=8米，
∴AB=DE+DC+BF=4+30+8=42米．
分析：（1）根据已知背水坡的坡度i₂可求得∠A的度数；
（2）过点C作CF⊥AB于F，从而得到DC=EF，DE=CF，再根据坡度求得BF的长，这样就不难求出AB的长．
点评：此题主要考查了学生对坡度坡角的理解及矩形的判定等知识点的掌握情况．