题目内容
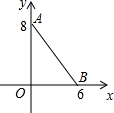 如图,点A的坐标为(0,8),点B的坐标为(6,0),在x轴上确定一点P,使△PAB为一个等腰三角形,则P点的坐标可以是
如图,点A的坐标为(0,8),点B的坐标为(6,0),在x轴上确定一点P,使△PAB为一个等腰三角形,则P点的坐标可以是(-
,0)或(-6,0)或(16,0)或(-4,0)
| 7 |
| 3 |
(-
,0)或(-6,0)或(16,0)或(-4,0)
.| 7 |
| 3 |
分析:分以AB为底、AB为腰A为顶点、AB为腰B为顶点三种情况讨论即可.
解答: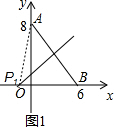 解:①以AB为底边时,
解:①以AB为底边时,
作AB的垂直平分线交x轴于点P1,
则P1A=P1B
设点P的坐标为(a,0)
则a2+82=(6-a)2
解得:a=-
∴P1(-
,0)
②当以AB为腰A为顶点时,
如图2,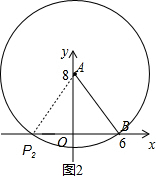 以A为圆心,以AB的长为半径作圆,交x轴于点P2,
以A为圆心,以AB的长为半径作圆,交x轴于点P2,
此时OB=OP2,
故p2的坐标为(-6,0)
③以AB为腰B为顶点时,如图3,以B为圆心以BA的长为半径作圆交x轴于点P3和P4,
此时BP3=BP4=AB=10,
∴点P3的坐标为(16,0),点P4的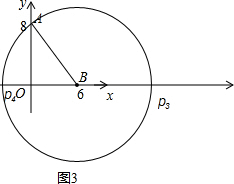 坐标为(-4,0)
坐标为(-4,0)
故答案为:(-
,0)或(-6,0)或(16,0)或(-4,0)
 解:①以AB为底边时,
解:①以AB为底边时,作AB的垂直平分线交x轴于点P1,
则P1A=P1B
设点P的坐标为(a,0)
则a2+82=(6-a)2
解得:a=-
| 7 |
| 3 |
∴P1(-
| 7 |
| 3 |
②当以AB为腰A为顶点时,
如图2,
 以A为圆心,以AB的长为半径作圆,交x轴于点P2,
以A为圆心,以AB的长为半径作圆,交x轴于点P2,此时OB=OP2,
故p2的坐标为(-6,0)
③以AB为腰B为顶点时,如图3,以B为圆心以BA的长为半径作圆交x轴于点P3和P4,
此时BP3=BP4=AB=10,
∴点P3的坐标为(16,0),点P4的
 坐标为(-4,0)
坐标为(-4,0)故答案为:(-
| 7 |
| 3 |
点评:本题考查了等腰三角形的判定,能够分三种情况分类讨论是解题的关键.

练习册系列答案
相关题目
 (2012•桂平市三模)如图,点P的坐标为(2,
(2012•桂平市三模)如图,点P的坐标为(2, 已知:在直角坐标系中,点C的坐标为(0,-2),点A与点B在x轴上,且点A与点B的横坐标是方程x2-3x-4=0的两个根,点A在点B的左侧.
已知:在直角坐标系中,点C的坐标为(0,-2),点A与点B在x轴上,且点A与点B的横坐标是方程x2-3x-4=0的两个根,点A在点B的左侧. 如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为
如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为 如图,点A的坐标为( )
如图,点A的坐标为( )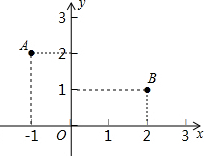 如图,点A的坐标为(-1,2),点B的坐标为(2,1),有一点C在x轴上移动,则点C到A、B两点的距离之和的最小值为( )
如图,点A的坐标为(-1,2),点B的坐标为(2,1),有一点C在x轴上移动,则点C到A、B两点的距离之和的最小值为( )