题目内容
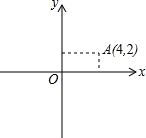⊙O的半径为4，如图圆心O的坐标为（0，0），点A的坐标为（4，2），则点A与⊙O的位置关系是
- A.点A在⊙O内
- B.点A在⊙O外
- C.点A在⊙O上
- D.不能确定
B
分析：本题先由勾股定理求得点A到圆心O的距离，再根据点与圆心的距离与半径的大小关系，来判断出点P与⊙O的位置关系即可．
解答：∵点A的坐标为（4，2），
∴由勾股定理得，点A到圆心O的距离AO=
=2
，
∵⊙O的半径为4，而4＜2，
即d＞r，
∴点A在圆外，
故选B．
点评：本题考查了点与圆的位置关系，判断的依据为当d＞r时，点在圆外；当d=r时，点在圆上；当d＜r时，点在圆内．
分析：本题先由勾股定理求得点A到圆心O的距离，再根据点与圆心的距离与半径的大小关系，来判断出点P与⊙O的位置关系即可．
解答：∵点A的坐标为（4，2），
∴由勾股定理得，点A到圆心O的距离AO=
=2，∵⊙O的半径为4，而4＜2
，即d＞r，
∴点A在圆外，
故选B．
点评：本题考查了点与圆的位置关系，判断的依据为当d＞r时，点在圆外；当d=r时，点在圆上；当d＜r时，点在圆内．
练习册系列答案
阅读快车系列答案
相关题目
BC上运动（与点B、C不重合），设BO=x，△AOC的面积为y．
点B、C不重合），设BO=x，△AOC的面积为y．
有一圆柱体高为8cm，底面圆的半径为2cm，如图所示，在AA1上的点Q处有一只蜘蛛，QA1=3cm，在BB1上的点P处有一只苍蝇，PB=2cm．