题目内容
 如图所示,在长方形ABCD中,E、F分别是AB、BC上的点,且BE=12,BF=16,则由点E到F的最短距离为
如图所示,在长方形ABCD中,E、F分别是AB、BC上的点,且BE=12,BF=16,则由点E到F的最短距离为
- A.20
- B.24
- C.28
- D.32
A
分析:要求由点E到F的最短距离,根据两点间线段最短,所以只需要求出线段EF的长即可.在Rt△EBF中,由勾股定理可求得EF的长.
解答:在Rt△EBF中,由勾股定理得:
EF2=BE2+BF2,
又BE=12,BF=16,
EF= =
=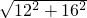 =20,
=20,
根据两点间线段最短可求出由点E到F的最短距离为20.
故选A.
点评:本题主要考查应用勾股定理求线段长度的能力,考查到的知识点有:两点间的线段最短及长方形的性质(长方形的四个角为直角).
分析:要求由点E到F的最短距离,根据两点间线段最短,所以只需要求出线段EF的长即可.在Rt△EBF中,由勾股定理可求得EF的长.
解答:在Rt△EBF中,由勾股定理得:
EF2=BE2+BF2,
又BE=12,BF=16,
EF=
 =
=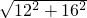 =20,
=20,根据两点间线段最短可求出由点E到F的最短距离为20.
故选A.
点评:本题主要考查应用勾股定理求线段长度的能力,考查到的知识点有:两点间的线段最短及长方形的性质(长方形的四个角为直角).

练习册系列答案
相关题目
 如图所示,在长方形ABCD中,E、F分别是AB、BC上的点,且BE=12,BF=16,则由点E到F的最短距离为( )
如图所示,在长方形ABCD中,E、F分别是AB、BC上的点,且BE=12,BF=16,则由点E到F的最短距离为( )| A、20 | B、24 | C、28 | D、32 |
 10、如图所示,在长方形ABCD的对称轴l上找点P,使得△PAB、△PBC均为等腰三角形,则满足条件的点P有( )
10、如图所示,在长方形ABCD的对称轴l上找点P,使得△PAB、△PBC均为等腰三角形,则满足条件的点P有( ) 如图所示,在长方形ABCD中,AB=3,BC=9,将图形沿着EF对折,使得B点与D点重合,A点落在A′的位置.
如图所示,在长方形ABCD中,AB=3,BC=9,将图形沿着EF对折,使得B点与D点重合,A点落在A′的位置. 如图所示,在长方形ABCD中,AB=16,BC=8,将长方形沿AC折叠,使D落在点E处,且CE与AB交于点F,求AF的长.
如图所示,在长方形ABCD中,AB=16,BC=8,将长方形沿AC折叠,使D落在点E处,且CE与AB交于点F,求AF的长. 如图所示,在长方形ABCD中,AB=10cm,BC=6cm,试问将长方形ABCD沿着AB方向平移多少才能使平移后的长方形与原来的长方形ABCD重叠部分的面积为24cm2?
如图所示,在长方形ABCD中,AB=10cm,BC=6cm,试问将长方形ABCD沿着AB方向平移多少才能使平移后的长方形与原来的长方形ABCD重叠部分的面积为24cm2?