题目内容
 如图,在平行四边形ABCD中,E为AB的中点,F为AD上一点,EF交AC于G,AF=2cm,DF=4cm,AG=3cm,则AC的长为
如图,在平行四边形ABCD中,E为AB的中点,F为AD上一点,EF交AC于G,AF=2cm,DF=4cm,AG=3cm,则AC的长为
- A.9cm
- B.14cm
- C.15cm
- D.18cm
C
分析:延长FG交CB的延长线于点H.根据平行四边形的性质,得BC=AD=6cm,BC∥AD.根据AAS可以证明△AFE≌△BHE,则BH=AF=2cm,再根据BC∥AD,得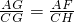 ,求得CG的长,从而求得AC的长.
,求得CG的长,从而求得AC的长.
解答: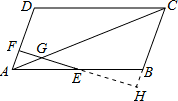 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,
∴BC=AD=6cm,BC∥AD.
∴∠EAF=∠EBH,∠AFE=∠BHE,
又AE=BE,
∴△AFE≌△BHE,
∴BH=AF=2cm.
∵BC∥AD,
∴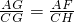 ,
,
即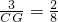 ,
,
则CG=12,
则AC=AG+CG=15(cm).
故选C.
点评:此题综合考查了平行四边形的性质、全等三角形的判定及性质、平行线分线段成比例定理.此题中要能够巧妙构造辅助线.
分析:延长FG交CB的延长线于点H.根据平行四边形的性质,得BC=AD=6cm,BC∥AD.根据AAS可以证明△AFE≌△BHE,则BH=AF=2cm,再根据BC∥AD,得
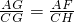 ,求得CG的长,从而求得AC的长.
,求得CG的长,从而求得AC的长.解答:
 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,∴BC=AD=6cm,BC∥AD.
∴∠EAF=∠EBH,∠AFE=∠BHE,
又AE=BE,
∴△AFE≌△BHE,
∴BH=AF=2cm.
∵BC∥AD,
∴
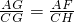 ,
,即
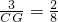 ,
,则CG=12,
则AC=AG+CG=15(cm).
故选C.
点评:此题综合考查了平行四边形的性质、全等三角形的判定及性质、平行线分线段成比例定理.此题中要能够巧妙构造辅助线.

练习册系列答案
相关题目
 如图,在平行四边形ABCD中,AB=2
如图,在平行四边形ABCD中,AB=2| 2 |
| 3 |
| 5 |
| A、AC⊥BD |
| B、四边形ABCD是菱形 |
| C、△ABO≌△CBO |
| D、AC=BD |
 17、如图,在平行四边形ABCD中,EF∥AD,GH∥AB,EF、GH相交于点O,则图中共有
17、如图,在平行四边形ABCD中,EF∥AD,GH∥AB,EF、GH相交于点O,则图中共有 如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,证明:四边形DFBE是平行四边形.
如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,证明:四边形DFBE是平行四边形. 的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米.
的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米. (2013•同安区一模)如图,在平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则AD的长为
(2013•同安区一模)如图,在平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则AD的长为