题目内容
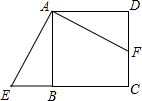如图，已知正方形ABCD的边长为4，延长CB到E，使BE=3，连接AE，过点A作AF⊥AE交DC于F（1）求证：△ADF≌△ABE
（2）求cos∠BAF的值．
分析：（1）由于四边形ABCD是正方形，那么∠BAD=90°，而AF⊥AE，利用同角的余角相等，可得∠DAF=∠EAB，又∠ABE=∠D=90°，AB=AD，故△ADF≌△ABE．
（2）根据△ADF≌△ABE，得出AE=AF，AH=DF=BE，即可求出cos∠BAF的值．
（2）根据△ADF≌△ABE，得出AE=AF，AH=DF=BE，即可求出cos∠BAF的值．
解答：
（1）证明：∵四边形ABCD是正方形，
∴∠BAD=∠DAF+∠BAF=90°，
又∵AF⊥AE，
∴∠EAB+∠BAF=90°，
∴∠DAF=∠EAB，
又∵四边形ABCD是正方形，
∴∠ABE=∠D=90°，AB=AD，
∴△ADF≌△ABE．
（2）解：过F作FH⊥AB于H，则四边形ABCD为矩形，AH=DF，
在Rt△ABE中，由勾股定理得：AE=5，
由（1）得△ADF≌△ABE，
∴AF=AE=5，AH=DF=BE=3，
∴在Rt△AHF中，cos∠BAF=
．
（1）证明：∵四边形ABCD是正方形，∴∠BAD=∠DAF+∠BAF=90°，
又∵AF⊥AE，
∴∠EAB+∠BAF=90°，
∴∠DAF=∠EAB，
又∵四边形ABCD是正方形，
∴∠ABE=∠D=90°，AB=AD，
∴△ADF≌△ABE．
（2）解：过F作FH⊥AB于H，则四边形ABCD为矩形，AH=DF，
在Rt△ABE中，由勾股定理得：AE=5，
由（1）得△ADF≌△ABE，
∴AF=AE=5，AH=DF=BE=3，
∴在Rt△AHF中，cos∠BAF=
| 3 |
| 5 |
点评：此题主要考查正方形的性质、全等三角形的判定与性质和勾股定理的运用．
练习册系列答案
相关题目
如图，已知正方形ABCD的边AB与正方形AEFM的边AM在同一直线上，直线BE与DM交于点N．求证：BN⊥DM．
（2013•北碚区模拟）如图，已知正方形ABCD，点E是BC上一点，点F是CD延长线上一点，连接EF，若BE=DF，点P是EF的中点．
如图，已知正方形ABCD，点E在BC边上，将△DCE绕某点G旋转得到△CBF，点F恰好在AB边上．
如图，已知正方形ABCD的对角线交于O，过O点作OE⊥OF，分别交AB、BC于E、F，若AE=4，CF=3，则EF的值是（ ）
如图，已知正方形ABCD的对角线AC，BD相交于点O，E是AC上的一点，过点A作AG⊥BE，垂足为G，AG交BD于点F．