题目内容
如图,一个直角三角形两条直角边分别为3cm和4cm,以斜边AB所在直线为轴旋转一周得到一个几何体,在虚线框内画出这个几何体的草图,求这个几何体的表面积.
分析:几何体的表面积是由上下两个圆锥的侧面积组成的,它们的底面半径相同,都是直角三角形斜边上的高,求得两个圆锥的侧面面积后求和.
解答: 解:如图,作OC交AB于O,则OC为两个圆锥共同的底面的半径,
解:如图,作OC交AB于O,则OC为两个圆锥共同的底面的半径,
AB=
=
=5,
∵AB•OC=AC•BC
∴OC=
,
以AC为母线的圆锥侧面积=
×2π×
×3=
π(cm2),
以BC为母线的圆锥侧面积=
×2π×
×4=
π(cm2),
∴表面积为
π+
π=
π(cm2).
 解:如图,作OC交AB于O,则OC为两个圆锥共同的底面的半径,
解:如图,作OC交AB于O,则OC为两个圆锥共同的底面的半径,AB=
| AC2+BC2 |
| 32+42 |
∵AB•OC=AC•BC
∴OC=
| 12 |
| 5 |
以AC为母线的圆锥侧面积=
| 1 |
| 2 |
| 12 |
| 5 |
| 36 |
| 5 |
以BC为母线的圆锥侧面积=
| 1 |
| 2 |
| 12 |
| 5 |
| 48 |
| 5 |
∴表面积为
| 36 |
| 5 |
| 48 |
| 5 |
| 84 |
| 5 |
点评:解决本题的关键是得到这个立体图形是由两个圆锥组成,以及相应的底面半径.

练习册系列答案
相关题目
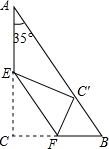 如图是一个直角三角形的纸片,将直角沿EF折叠,使C点落在AB边上,并且使∠EC′A=∠A,那么∠C′FE的度数是( )
如图是一个直角三角形的纸片,将直角沿EF折叠,使C点落在AB边上,并且使∠EC′A=∠A,那么∠C′FE的度数是( )| A、50° | B、45° | C、55° | D、70°第7题图 |
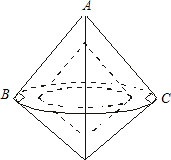 如图,一个直角三角形纸板,其两条直角边长分别为6cm和8cm,小明以纸板的斜边为旋转轴旋转这个三角形纸板形成如图所示的旋转体.请你帮小明推算出这个旋转体的全面积.(π取3.14)
如图,一个直角三角形纸板,其两条直角边长分别为6cm和8cm,小明以纸板的斜边为旋转轴旋转这个三角形纸板形成如图所示的旋转体.请你帮小明推算出这个旋转体的全面积.(π取3.14)
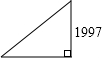 如图,一个直角三角形的三边长均为正整数,已知它的一条直角边的长恰是1997,那么另一条直角边的长为
如图,一个直角三角形的三边长均为正整数,已知它的一条直角边的长恰是1997,那么另一条直角边的长为 如图,一个直角三角形的三边长均为正整数,已知它的一条直角边的长恰是3,那么另一条直角边的长是
如图,一个直角三角形的三边长均为正整数,已知它的一条直角边的长恰是3,那么另一条直角边的长是