题目内容
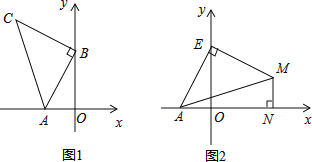
【题目】如图1,![]() ,
,![]() ,以B点为直角顶点在第二象限作等腰直角
,以B点为直角顶点在第二象限作等腰直角![]() .
.
![]() 求C点的坐标;
求C点的坐标;
![]() 在坐标平面内是否存在一点P,使
在坐标平面内是否存在一点P,使![]() 与
与![]() 全等?若存在,直接写出P点坐标,若不存在,请说明理由;
全等?若存在,直接写出P点坐标,若不存在,请说明理由;
![]() 如图2,点E为y轴正半轴上一动点,以E为直角顶点作等腰直角
如图2,点E为y轴正半轴上一动点,以E为直角顶点作等腰直角![]() ,过M作
,过M作![]() 轴于N,直接写出
轴于N,直接写出![]() 的值为 .
的值为 .
【答案】(1)![]() .(2)存在,P的坐标是
.(2)存在,P的坐标是![]() 或
或![]() 或
或![]() 或
或![]() .(3)1.
.(3)1.
【解析】
![]() 作
作![]() 轴于E,证
轴于E,证![]() ≌
≌![]() ,推出
,推出![]() ,
,![]() ,即可得出答案;
,即可得出答案;
![]() 分为四种情况,画出符合条件的图形,构造直角三角形,证三角形全等,即可得出答案;
分为四种情况,画出符合条件的图形,构造直角三角形,证三角形全等,即可得出答案;
![]() 作
作![]() 轴于F,证
轴于F,证![]() ≌
≌![]() ,求出EF,即可得出答案.
,求出EF,即可得出答案.
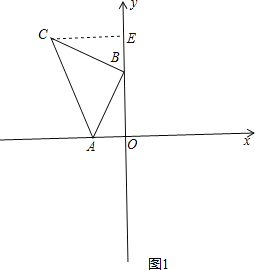
![]() 作
作![]() 轴于E,如图1,
轴于E,如图1,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
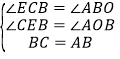 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
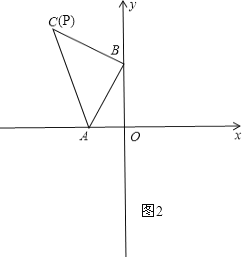
即![]() ,
,
![]() .
.
![]() 存在一点P,使
存在一点P,使![]() 与
与![]() 全等,
全等,
分为四种情况:![]() 如图2,当P和C重合时,
如图2,当P和C重合时,![]() 和
和![]() 全等,即此时P的坐标是
全等,即此时P的坐标是![]() ;
;
![]() 如图3,过P作
如图3,过P作![]() 轴于E,
轴于E,
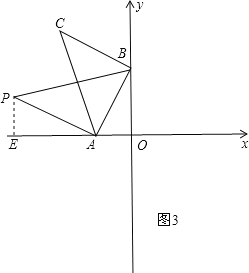
则![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中
中
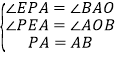 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
即P的坐标是![]() ;
;
![]() 如图4,过C作
如图4,过C作![]() 轴于M,过P作
轴于M,过P作![]() 轴于E,
轴于E,
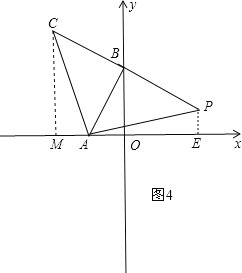
则![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
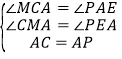 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
即P的坐标是![]() ;
;
![]() 如图5,过P作
如图5,过P作![]() 轴于E,
轴于E,
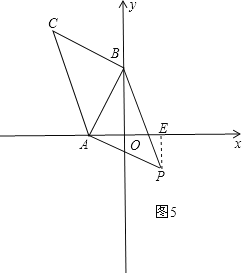
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
则![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
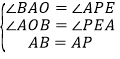 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
即P的坐标是![]() ,
,
综合上述:符合条件的P的坐标是![]() 或
或![]() 或
或![]() 或
或![]() .
.
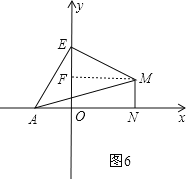
![]() 如图6,作
如图6,作![]() 轴于F,
轴于F,
则![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中
中
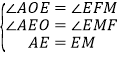 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() 轴,
轴,![]() 轴,
轴,
![]() ,
,
![]() 四边形FONM是矩形,
四边形FONM是矩形,
![]() ,
,
![]() .
.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目