题目内容
如图,在平面直角坐标系xOy中,⊙P与y轴
相切于点C,⊙P的半径是4,直线 被⊙P
被⊙P
截得的弦AB的长为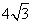 ,求点P的坐标.
,求点P的坐标.
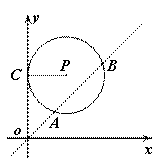
解:延长CP交AB于点E,过点P做PD⊥AB于D
∴AD=BD= =
=
连接PA
在△PDA中,∠PDA=90°,PA=4,AD=
∴PD=2 ---------------------1分
∵⊙P与y轴相切于点C
 ∴PC⊥y轴,
∴PC⊥y轴,
∴∠OCE=90° ----------------2分
∵直线y=x,
∴∠COE=45° ------------------3分
∴∠CEO=45°,OC=CE
在△PDE中,∠PDE=90°,PD=2,∴PE=
∴CE=4+ ,∴OC=4+
,∴OC=4+ --------------------------------------4分
--------------------------------------4分
∴点P的坐标为:P(4,4+ )-------------------------------------5分
)-------------------------------------5分

 名校课堂系列答案
名校课堂系列答案有这样一个问题:探究函数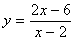 的图象与性质.
的图象与性质.
小慧根据学习函数的经验,对函数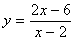 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小慧的探究过程,请补充完成:
(1)函数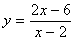 的自变量x的取值范围是___________;
的自变量x的取值范围是___________;
(2)列出y与x的几组对应值.请直接写出m的值,m=__________;
| x | … | -3 | -2 | 0 | 1 | 1.5 | 2.5 | m | 4 | 6 | 7 | … |
| y | … | 2.4 | 2.5 | 3 | 4 | 6 | -2 | 0 | 1 | 1.5 | 1.6 | … |
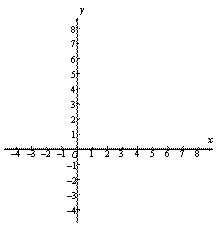
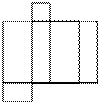
(3)请在平面直角坐标系 中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)结合函数的图象,写出该函数的两条性质:
① ;
 |
② .

 与
与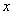 的一些对应值:
的一些对应值: 
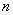
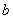 ,
,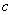 ,
,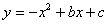 ,直接写出
,直接写出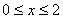 时
时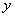 的最大值.
的最大值.



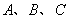 分别表示数
分别表示数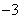 、
、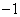 、
、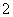 .
.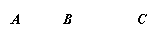

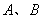 两点的距离
两点的距离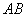 = ,
= ,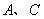 两点的距离AC= ;
两点的距离AC= ;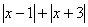 的最小值= .
的最小值= .