题目内容
已知平行于x轴的直线y=a(a≠0)与函数y=x和函数y=![]() 的图象分别交于点A和点B,又有定点P(2,0).
的图象分别交于点A和点B,又有定点P(2,0).

(1)若a>0,且tan∠POB=![]() ,求线段AB的长;
,求线段AB的长;
(2)在过A,B两点且顶点在直线y=x上的抛物线中,已知线段AB=![]() ,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
(3)已知经过A,B,P三点的抛物线,平移后能得到y=![]() x2的图象,求点P到直线AB的距离.
x2的图象,求点P到直线AB的距离.
答案:
解析:
解析:
|
(1)设第一象限内的点B(m,n),则tan∠POB 而AB∥x轴,所以点A( (2)由条件可知所求抛物线开口向下,设点A(a,a),B( 所以3a2+8a-3=0,解得 当a=-3时,点A(-3,-3),B(- 同理,当a= (3)设A(a,a),B( 设所求二次函数解析式为: 点A(a,a)代入,解得a1=3, |

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
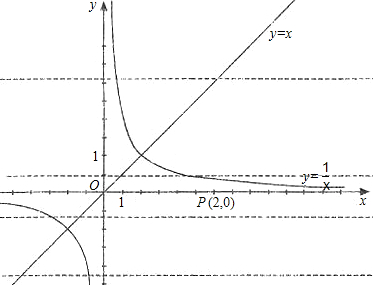
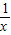 的图象分别交于点A和点B,又有定点P(2,0).
的图象分别交于点A和点B,又有定点P(2,0). ,求线段AB的长;
,求线段AB的长; ,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式; x2的图象,求点P到直线AB的距离.
x2的图象,求点P到直线AB的距离.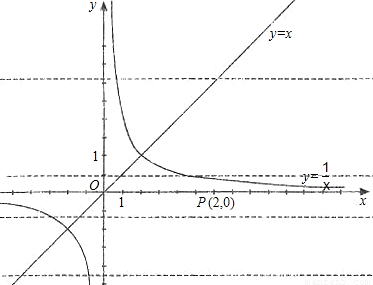
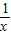 的图象分别交于点A和点B,又有定点P(2,0).
的图象分别交于点A和点B,又有定点P(2,0). ,求线段AB的长;
,求线段AB的长; ,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式; x2的图象,求点P到直线AB的距离.
x2的图象,求点P到直线AB的距离.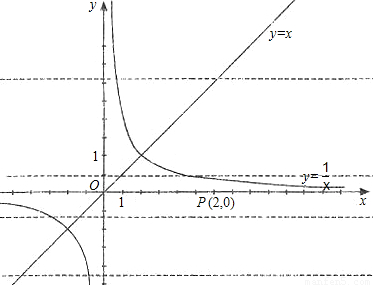
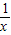 的图象分别交于点A和点B,又有定点P(2,0).
的图象分别交于点A和点B,又有定点P(2,0). ,求线段AB的长;
,求线段AB的长; ,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式; x2的图象,求点P到直线AB的距离.
x2的图象,求点P到直线AB的距离.
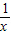 的图象分别交于点A和点B,又有定点P(2,0).
的图象分别交于点A和点B,又有定点P(2,0). ,求线段AB的长;
,求线段AB的长; ,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式; x2的图象,求点P到直线AB的距离.
x2的图象,求点P到直线AB的距离.