题目内容
已知抛物线y=mx2-4mx+4m-2(m是常数).(1)求抛物线的顶点坐标;
(2)若
| 1 | 5 |
分析:(1)根据抛物线y=ax2+bx+c的顶点(-
,
)即可得出答案;
(2)根据题意得出mx2-4mx+4m-2=0的根是整数.再由求根公式求出两根,根据m的取值得出抛物线的解析式为y=2x2-8x+6或y=
x2-2x或y=
x2-
x-
.
| b |
| 2a |
| 4ac-b2 |
| 4a |
(2)根据题意得出mx2-4mx+4m-2=0的根是整数.再由求根公式求出两根,根据m的取值得出抛物线的解析式为y=2x2-8x+6或y=
| 1 |
| 2 |
| 2 |
| 9 |
| 8 |
| 9 |
| 10 |
| 9 |
解答:解:(1)依题意,得m≠0,
∴x=-
=-
=2,
y=
=
=
=-2.
∴抛物线的顶点坐标为(2,-2).(2分)
(2)∵抛物线与x轴交于整数点,
∴mx2-4mx+4m-2=0的根是整数.
∴x=
=2±
.
∵m>0,
∴x=2±
是整数.(3分)
∴
是完全平方数.
∵
<m<5,
∴
<
<10(4分)
∴
取1,4,9,
当
=1时,m=2;
当
=4时,m=
;
当
=9时,m=
.
∴m的值为2或
或
.
∴抛物线的解析式为y=2x2-8x+6或y=
x2-2x或y=
x2-
x-
.(7分)
∴x=-
| b |
| 2a |
| -4m |
| 2m |
y=
| 4ac-b2 |
| 4a |
| 4m(4m-2)-(-4m)2 |
| 4m |
| 16m2-8m-16m2 |
| 4m |
∴抛物线的顶点坐标为(2,-2).(2分)
(2)∵抛物线与x轴交于整数点,
∴mx2-4mx+4m-2=0的根是整数.
∴x=
4m±
| ||
| 2m |
2
| ||
| 2m |
∵m>0,
∴x=2±
|
∴
| 2 |
| m |
∵
| 1 |
| 5 |
∴
| 2 |
| 5 |
| 2 |
| m |
∴
| 2 |
| m |
当
| 2 |
| m |
当
| 2 |
| m |
| 1 |
| 2 |
当
| 2 |
| m |
| 2 |
| 9 |
∴m的值为2或
| 1 |
| 2 |
| 2 |
| 9 |
∴抛物线的解析式为y=2x2-8x+6或y=
| 1 |
| 2 |
| 2 |
| 9 |
| 8 |
| 9 |
| 10 |
| 9 |
点评:本题考查了抛物线与x轴的交点问题、用待定系数法求二次函数的解析式,以及二次函数的性质.

练习册系列答案
相关题目
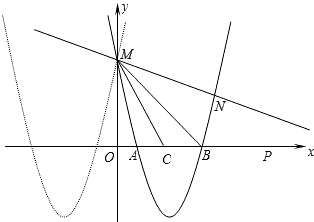 点N(a,b),a,b满足a2-a+m=0,b2-b+m=0,则点N的坐标为
点N(a,b),a,b满足a2-a+m=0,b2-b+m=0,则点N的坐标为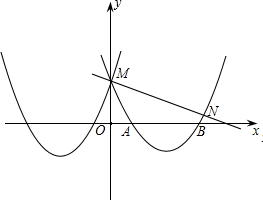 点M,与x轴交于点A和B.
点M,与x轴交于点A和B. 如图,已知抛物线y=mx2+nx+p与y=x2+6x+5关于y轴对称,并与y轴交于点M,与x轴交于点A和B.
如图,已知抛物线y=mx2+nx+p与y=x2+6x+5关于y轴对称,并与y轴交于点M,与x轴交于点A和B.