Question

【题目】平面内有任意一点和，按要求解答下列问题：

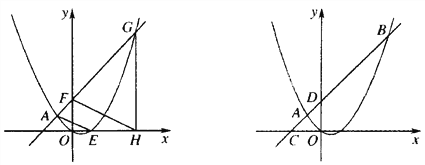
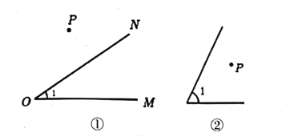
（1）当点和外部时，如图①，过点作，，垂足分别为、，量一量和的度数，用数学式子表达它们之间的数量关系 ；

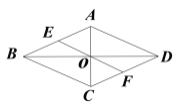
（2）当点在内部时，如图②，以点为顶点作，使的两边分别和的两边垂直，垂足分别为、，用数学式子写出和的数量关系；

（3）由上述情形，用文字语言叙述结论：如果一个角的两边分别和另一个角的两边垂直，那么这两个角 .

（4）在图②中，若，求的度数.

Answer 1

【答案】（1）=；（2）∠1+∠APB =180°（3）相等或互补.（4）∠APB=

【解析】

（1）根据测量结果，比较判断即可；

（2）根据测量数据可以得出结论，也可以通过四边形内角和来计算解决；

（3）根据（1）（2）得出的结果判断，回答即可；

（4）利用（3）的结论，判断即可.

解：如图所示，（1）经过测量，我们发现：=；

（2）∵PA、PB分别垂直OB、OA

∴∠OAP=∠OBP=90°

又∵四边形AOBP的内角和为360°，

∴∠1+∠APB=360°-∠OAP-∠OBP=180°

（3）由（1）、（2）情形可知：如果一个角的两边分别和另一个角的两边垂直，那么这两个角相等或互补.

（4）由（3）的结论可知

∠1=∠APB

∵，

∴∠APB=