题目内容
函数y=（k+2）x+k2-4经过原点，则k=
2
2
．分析：直接把（0，0）代入函数y=（k+2）x+k2-4求出k的值即可．
解答：解：∵函数y=（k+2）x+k2-4经过原点，
∴0=k2-4，解得k=±2，
∵y=（k+2）x+k2-4是一次函数数，
∴k+2≠0，即k≠-2．
∴k=2．
故答案为：2．
∴0=k2-4，解得k=±2，
∵y=（k+2）x+k2-4是一次函数数，
∴k+2≠0，即k≠-2．
∴k=2．
故答案为：2．
点评：本题考查的是一次函数图象上点的坐标特点，熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．
练习册系列答案
智慧小复习系列答案
相关题目
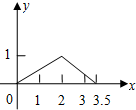
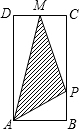如图，矩形ABCD中，AB=1，AD=2，M是CD的中点，点P在矩形的边上沿A?B?C?M运动，则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是下图中的（ ）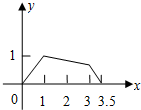
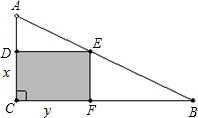为60米和120米．现准备在AB上选一个点E，在空地中（如图所示）挖掘建造一个矩形游泳池．函数y=
中自变量x的取值范围是（ ）
| ||
| x |
A、x≤
| ||
B、x＞-
| ||
| C、x≠0 | ||
D、x＜
|