题目内容
【题目】如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连接PD.
(1)求点B的坐标;
(2)当∠CPD=∠OAB,且![]() ,求这时点P的坐标.
,求这时点P的坐标.
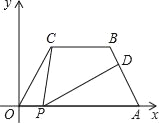
【答案】(1) 点B的坐标为(5,![]() );(2) 点P坐标为(1,0)或(6,0).
);(2) 点P坐标为(1,0)或(6,0).
【解析】
(1)依题意可得∠BAQ=∠COA,已知AB=4,∠COA度数利用三角函数可求出BQ,AQ,OQ的值.
(2)利用相似三角形的判定证明△OCP∽△APD,根据等比性质可求出AP,OP的值.
解:(1)作BQ⊥x轴于Q.
∵四边形OABC是等腰梯形,
∴∠BAQ=∠COA=60°
在Rt△BQA中,BA=4,
BQ=ABsin∠BAO=4×sin60°=![]()
AQ=ABcos∠BAO=4×cos60°=2,
∴OQ=OA﹣AQ=7﹣2=5
点B在第一象限内,∴点B的坐标为(5,![]() );
);
(2)∵∠CPA=∠OCP+∠COP,
即∠CPD+∠DPA=∠COP+∠OCP,
而∠CPD=∠OAB=∠COP=60°,
∴∠OCP=∠APD.
∵∠COP=∠PAD,
∴△OCP∽△APD.
∴![]() .
.
∴OPAP=OCAD.
∵![]() ,且AB=4,
,且AB=4,
∴BD=![]() AB=
AB=![]() ,
,
AD=AB﹣BD=4﹣![]() =
=![]() .
.
∵AP=OA﹣OP=7﹣OP,
∴OP(7﹣OP)=4×![]() ,
,
解得:OP=1或6.
∴点P坐标为(1,0)或(6,0).
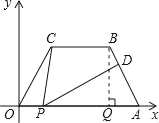
故答案为:(1) 点B的坐标为(5,![]() );(2) 点P坐标为(1,0)或(6,0).
);(2) 点P坐标为(1,0)或(6,0).

练习册系列答案
相关题目