Question

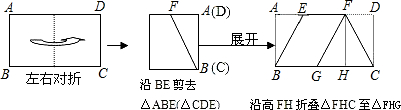
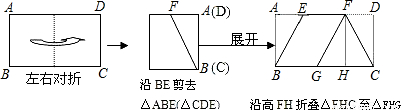
.如图，将一张矩形纸片ABCD沿直线MN折叠，使点C落在点A处，点D落在点E处，直线MN交BC于点M，交AD于点N.

（1）求证：CM=CN；

（2）若ΔCMN的面积与ΔCDN的面积比为3：1，求的值.

Answer 1

解：（1）证明：∵ 四边形AMNE是由四边形CMND折叠而得，且点C                 与点A重合.

             ∴

              四边形ABCD是矩形

             ∴AD//BC.

              

             ∴

             ∴CM=CN.

(2)过点N作NH┴BC,垂足为H,则四边形NHCD是矩形，∴HC=DN，NH＝DC。

∵ΔＣＭＮ的面积与ΔCDN的面积比是３：１，∴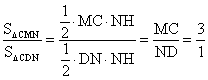

∴MC＝３ND＝３HC，MH＝２HC。设DN＝x，则HC=x，MH=2x,∴CM=3x=CN;在RtΔCDN中，，∴HN=。同理：，∴。