Question

【题目】在⊙O中，直径AB=6，BC是弦，∠ABC=30°，点P在BC上，点Q在⊙O上，且OP⊥PQ．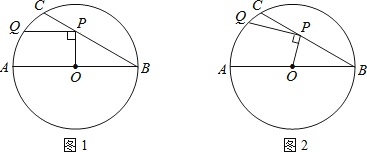

（1）如图1，当PQ∥AB时，求PQ的长度；
（2）如图2，当点P在BC上移动时，求PQ长的最大值．

Answer 1

【答案】
（1）

【解答】解：（1）连结OQ，如图1，

∵PQ∥AB，OP⊥PQ，

∴OP⊥AB，

在Rt△OBP中，∵tan∠B=，

∴OP=3tan30°=，

在Rt△OPQ中，∵OP=，OQ=3，

∴PQ==；

（2）

（2）连结OQ，如图2，

在Rt△OPQ中，PQ==，

当OP的长最小时，PQ的长最大，

此时OP⊥BC，则OP=OB=，

∴PQ长的最大值为=．

【解析】（1）连结OQ，如图1，由PQ∥AB，OP⊥PQ得到OP⊥AB，在Rt△OBP中，利用正切定义可计算出OP=3tan30°=，然后在Rt△OPQ中利用勾股定理可计算出PQ=；
（2）连结OQ，如图2，在Rt△OPQ中，根据勾股定理得到PQ=，则当OP的长最小时，PQ的长最大，根据垂线段最短得到OP⊥BC，则OP=OB=，所以PQ长的最大值=．
【考点精析】本题主要考查了勾股定理的概念和圆周角定理的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题．