题目内容
如图，反比例函数y1=| k1 |
| x |
| k1 |
| x |
x＜-1或0＜x＜1
x＜-1或0＜x＜1
．分析：所求不等式的解集即为反比例函数值大于一次函数值时x的范围，根据一次函数与反比例函数的交点坐标，即可确定出x的范围．
解答：解：根据反比例函数y1=
和正比例函数y2=k2x的图象交于A（-1，-3）、B（1，3）两点，
利用图象得：
＞k2x时x的取值范围是x＜-1或0＜x＜1．
故答案为：x＜-1或0＜x＜1
| k1 |
| x |
利用图象得：
| k1 |
| x |
故答案为：x＜-1或0＜x＜1
点评：此题考查了反比例函数与一次函数的交点问题，利用了数形结合的思想，熟练运用数形结合思想是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
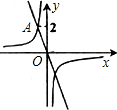如图，反比例函数y1=| k |
| x |
| A、-2＜X＜2 |
| B、-1＜x＜0或x＞1 |
| C、x＜-1或0＜x＜1 |
| D、x＜-1或x＞1 |
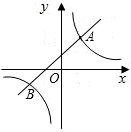如图，反比例函数
（2012•滦南县一模）如图，反比例函数
已知如图：反比例函数
如图，反比例函数y1=