题目内容
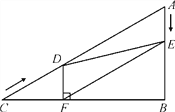
【题目】如图,某河的两岸PQ、MN互相平行,河岸PQ上的点A处和点B处各有一棵大树,AB=30米,某人在河岸MN上选一点C,AC⊥MN,在直线MN上从点C前进一段路程到达点D,测得∠ADC=30°,∠BDC=60°,求这条河的宽度.( ![]() ≈1.732,结果保留三个有效数字).
≈1.732,结果保留三个有效数字).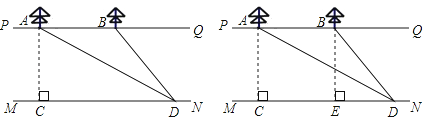
【答案】解:过点B作BE⊥MN于点E,则CE=AB=30米,CD=CE+ED,AC=BE,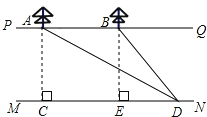
设河的宽度为x,
在Rt△ACD中,
∵AC⊥MN,CE=AB=30米,∠ADC=30°,
∴ ![]() =tan∠ADC,即
=tan∠ADC,即 ![]() ①,
①,
在Rt△BED中,![]() =tan∠BDC,
=tan∠BDC, ![]() =
= ![]() ②,
②,
①②联立得,x=15 ![]() ≈26.0(米).
≈26.0(米).
答:这条河的宽度为26.0米.
【解析】过点B作BE⊥MN于点E,则CE=AB=30米,CD=CE+ED,AC=BE,在Rt△ACD中,由锐角三角函数的定义可知, ![]() =tan∠ADC,在Rt△BED中,
=tan∠ADC,在Rt△BED中, ![]() =tan∠BDC,两式联立即可得出AC的值,即这条河的宽度.
=tan∠BDC,两式联立即可得出AC的值,即这条河的宽度.
【考点精析】通过灵活运用关于方向角问题,掌握指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角即可以解答此题.

练习册系列答案
相关题目