题目内容
 11、如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么⊙P与直线CD相切时运动时间为( )
11、如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么⊙P与直线CD相切时运动时间为( )分析:只要注意此题可分两种情况当点P在OA上时、当点P在OB上时,则易解.
解答: 解:作PE⊥CD于E.若⊙P与直线CD相切,则PE=1,
解:作PE⊥CD于E.若⊙P与直线CD相切,则PE=1,
当点P在OA上时,此时OP=2PE=2,则⊙P需要移动6-2=4cm,需要时间4秒;
当点P在OB上时,此时OP=2PE=2,则⊙P需要移动6+2=8cm,需要时间8秒.
故选D.
 解:作PE⊥CD于E.若⊙P与直线CD相切,则PE=1,
解:作PE⊥CD于E.若⊙P与直线CD相切,则PE=1,当点P在OA上时,此时OP=2PE=2,则⊙P需要移动6-2=4cm,需要时间4秒;
当点P在OB上时,此时OP=2PE=2,则⊙P需要移动6+2=8cm,需要时间8秒.
故选D.
点评:此题注意考虑两种情况:点P在O的左侧或在O的右侧.掌握直线和圆相切应满足的数量关系,熟练运用特殊三角形的性质:30°所对的直角边是斜边的一半.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 21、如图,直线AB、CD、EF都经过点O,且AB⊥CD,∠COE=35°,求∠DOF、∠BOF的度数.
21、如图,直线AB、CD、EF都经过点O,且AB⊥CD,∠COE=35°,求∠DOF、∠BOF的度数.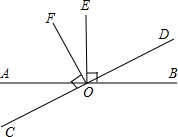 如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.
如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.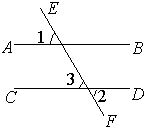 25、完成推理填空:如图:直线AB、CD被EF所截,若已知AB∥CD,
25、完成推理填空:如图:直线AB、CD被EF所截,若已知AB∥CD, 如图,直线AB、CD、EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=24°,∠COG的度数=
如图,直线AB、CD、EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=24°,∠COG的度数= 如图,直线AB,CD相交于O点,EO⊥CD,垂足为O点,若∠BOE=50°,求∠AOD的度数.
如图,直线AB,CD相交于O点,EO⊥CD,垂足为O点,若∠BOE=50°,求∠AOD的度数.