Question

【题目】如图，一艘船以每小时30海里的速度向北偏东75°方向航行，在点A处测得码头C在船的东北方向，航行40分钟后到达B处，这时码头C恰好在船的正北方向，在船不改变航向的情况下，求出船在航行过程中与码头C的最近距离．（结果精确的0.1海里，参考数据 ≈1.41， ≈1.73）

Answer 1

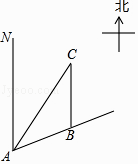
【答案】解：过点C作CE⊥AB于点E，过点B作BD⊥AC于点D，

由题意可知：船在航行过程中与码头C的最近距离是CE，
AB=30× =20，
∵∠NAC=45°，∠NAB=75°，
∴∠DAB=30°，
∴BD= AB=10，
由勾股定理可知：AD=10
∵BC∥AN，
∴∠BCD=45°，
∴CD=BD=10，
∴AC=10 +10
∵∠DAB=30°，
∴CE= AC=5 +5≈13.7
答：船在航行过程中与码头C的最近距离是13.7海里
【解析】过点C作CE⊥AB于点E，过点B作BD⊥AC于点D，由题意可知：船在航行过程中与码头C的最近距离是CE，根据∠DAB=30°，AB=20，从而可求出BD、AD的长度，进而可求出CE的长度．