题目内容
如图，在△ABC中，AB＝AC，AD是△ABC的角平分线，点O为AB的中点，连接DO并延长到点E，使OE＝OD，连接AE，BE.
(1)求证：四边形AEBD是矩形；
(2)当△ABC满足什么条件时，矩形AEBD是正方形，并说明理由．
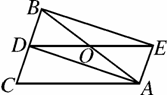
(1)证明：
∵点O为AB的中点，OE＝OD，
∴四边形AEBD是平行四边形． （2分）
∵AB＝AC，AD是△ABC的角平分线，
∴AD⊥BC.即∠ADB＝90°. （2分）
∴四边形AEBD是矩形． （1分）
(2)解：
当△ABC是等腰直角三角形时，
矩形AEBD是正方形． （1分）
∵△ABC是等腰直角三角形，
∴∠BAD＝∠CAD＝∠DBA＝45°.
∴BD＝AD. （2分）
由(1
)知四边形AEBD是矩形，
∴四边形AEBD是正方形． （2分）
练习册系列答案
相关题目
P为圆心，
为半径的圆与直线
：
相切，则符合条件的所有点P的坐标是_______________________．
BC，并在图3中画出相应的图形；
∠DBC值的大小变化情况，并给出你的证明．
是一个完全平方式，则
=_______
