题目内容
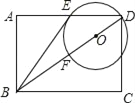
【题目】如图1所示,![]() 为矩形
为矩形![]() 的边
的边![]() 上一点,动点
上一点,动点![]() 同时从点
同时从点![]() 出发,点
出发,点![]() 沿折线
沿折线![]() 运动到点
运动到点![]() 时停止,点
时停止,点![]() 沿
沿![]() 运动到点
运动到点![]() 时停止,它们运动的速度都是
时停止,它们运动的速度都是![]() 秒.设
秒.设![]() 同时出发
同时出发![]() 秒时,
秒时,![]() 的面积为
的面积为![]() ,已知
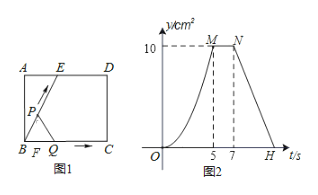
,已知![]() 与
与![]() 的函数关系图象如图2所示.请回答:
的函数关系图象如图2所示.请回答:
(1)线段![]() 的长为_______cm;
的长为_______cm;
(2)当运动时间![]() 秒时,
秒时,![]() 之间的距离是_______
之间的距离是_______![]() .
.
【答案】5 ![]()
【解析】
(1)根据图2可以判断三角形的面积变化分为三段,可以判断出当点P到达点E时点Q到达点C,从而得到BC的长度;
(2)如图1,过点P作PF⊥BC于点F,根据面积不变时△BPQ的面积为10,可得AB=4,由矩形的性质和锐角三角函数的定义求得PF的长度,然后在直角△PBF中,由勾股定理求得BF=1.5,再在直角△PFQ中,由勾股定理求得PQ的长度.
解:(1)根据图2可得,当点P到达点E时,点Q到达点C,
∵点P、Q的运动的速度都是1cm/s,
∴BC=BE=5cm,
故答案是:5;
(2)如图1,过点P作PF⊥BC于点F,
根据面积不变时△BPQ的面积为10,可得AB=4,
∵AD∥BC,
∴∠AEB=∠PBF,
∴sin∠PBF=sin∠AEB=![]() ,
,
∴PF=PBsin∠PBF=2.5×![]()
∴在直角△PBF中,由勾股定理得到:BF=![]() ,
,
∴FQ=2.5-1.5=1,
∴在直角△PFQ中,由勾股定理得到:PQ=![]() ,
,
故答案是:![]() .
.


练习册系列答案
相关题目