Question

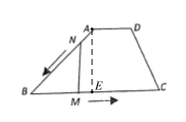
【题目】如图，在梯形ABCD中，AD//BC，,,,,动点M从B点出发沿线段BC以每秒2个单位长度的速度向C运动；动点N同时从A点出发沿线段AB以每秒1个单位长度的速度向B运动，其中一点到达终点时，则两点同时停止运动.设运动的时间为t秒，当△MNB为等腰直角三角形时，t的值是_______.

Answer 1

【答案】或

【解析】

根据∠C=60°，DC=2，可求出梯形的高，由∠B=45°可求出AB的长，根据题意当△MNB为等腰直角三角形时，BM=2t，AN=t，BN=BM或BM=BN，根据等量关系列出方程即可求解.

过A作AE⊥BC，

∵∠C=60°，DC=2，

∴AE=DCsin60°=3，

∴AB=6，

∵当∠BMN=90°时，BM=2t，AN=t，BN=BM，

∴AB-AN=BM，即6-t=2t，

t= ，

当∠BNM=90°时，BM=BN ，BM=2t，AN=t，

∴2t =（6-t），

t=6-6，

故答案为：6-6或