题目内容
设 ,
, 是任意两个不等实数,我们规定:满足不等式
是任意两个不等实数,我们规定:满足不等式 ≤
≤ ≤
≤ 的实数
的实数 的所有取值的全体叫做闭区间,表示为
的所有取值的全体叫做闭区间,表示为 . 对于一个函数,如果它的自变量
. 对于一个函数,如果它的自变量 与函数值
与函数值 满足:当m≤
满足:当m≤ ≤n时,有m≤
≤n时,有m≤ ≤n,我们就称此函数是闭区间
≤n,我们就称此函数是闭区间 上的“闭函数”.
上的“闭函数”.
(1)反比例函数 是闭区间
是闭区间 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由;
(2)若一次函数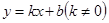 是闭区间
是闭区间 上的“闭函数”,求此函数的表达式;
上的“闭函数”,求此函数的表达式;
(3)若二次函数 是闭区间
是闭区间 上的“闭函数”,直接写出实数
上的“闭函数”,直接写出实数 ,
, 的值.
的值.
(1)是,理由见解析;(2)y=x或 ;(3)
;(3) 或
或 .
.
解析试题分析:(1)根据反比例函数 的单调区间进行判断.
的单调区间进行判断.
(2)根据新定义运算法则列出关于系数k、b的方程组 或
或 ,通过解该方程组即可求得系数k、b的值.
,通过解该方程组即可求得系数k、b的值.
(3)因为 ,所以该二次函数的图象开口方向向上,最小值是
,所以该二次函数的图象开口方向向上,最小值是 ,且当x<2时,y随x的增大而减小;当x>2时,y随x的增大而增大;根据新定义运算法则分三种情况列出关于系数a、b的方程组,解方程组即可求得a、b的值.
,且当x<2时,y随x的增大而减小;当x>2时,y随x的增大而增大;根据新定义运算法则分三种情况列出关于系数a、b的方程组,解方程组即可求得a、b的值.
(1)反比例函数 是闭区间[1,2014]上的“闭函数”. 理由如下:
是闭区间[1,2014]上的“闭函数”. 理由如下:
∵反比例函数 在第一象限,y随x的增大而减小,且
在第一象限,y随x的增大而减小,且
当x=1时,y=2014;当x=2014时,y=1,
∴当1≤x≤2014时,有1≤y≤2014,符合闭函数的定义,故反比例函数 是闭区间[1,2014]上的“闭函数”.
是闭区间[1,2014]上的“闭函数”.
(2)分两种情况:k>0或k<0.
①当k>0时,一次函数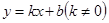 的图象是y随x的增大而增大,根据“闭函数”的定义得,
的图象是y随x的增大而增大,根据“闭函数”的定义得, ,解得
,解得 .
.
∴此函数的解析式是y=x.
②当k<0时,一次函数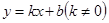 的图象是y随x的增大而减小,根据“闭函数”的定义得,
的图象是y随x的增大而减小,根据“闭函数”的定义得, ,解得
,解得 .
.
∴此函数的解析式是 .
.
(3)∵ ,
,
∴该二次函数的图象开口方向向上,最小值是 ,且当x<2时,y随x的增大而减小;当x>2时,y随x的增大而增大.
,且当x<2时,y随x的增大而减小;当x>2时,y随x的增大而增大.
①当b≤2时,此二次函数y随x的增大而减小,则根据“闭函数”的定义得, ,解得,
,解得, (不合题意,舍去)或
(不合题意,舍去)或 .
.
②当a<2<b时,此时二次函数 的最小值是
的最小值是 =a,根据“闭函数”的定义得
=a,根据“闭函数”的定义得 或
或 .
.
a)当 时,由于
时,由于 ,不合题意,舍去;
,不合题意,舍去;
b)当 时,解得
时,解得 ,
,
∵b>2,∴ .
.
③当a≥2时,此二次函数y随x的增大而增大,则根据“闭函数”的定义得, ,解得,
,解得, .
.
∵ <0,∴舍去.
<0,∴舍去.
综上所述, 或
或 .
.
考点:1.新定义;2.反比例函数、一次函数和二次函数的性质;3.解二元方程组;4.分类思想的应用.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案为了节约资源,科学指导居民改善居住条件,小王向房管部门提出了一个购买商品房的政策性方案.
| 人均住房面积(平方米) | 单价(万元/平方米) |
| 不超过30(平方米) | 0.3 |
| 超过30平方米不超过m(平方米)部分(45≤m≤60) | 0.5 |
| 超过m平方米部分 | 0.7 |
根据这个购房方案:
(1)若某三口之家欲购买120平方米的商品房,求其应缴纳的房款;
(2)设该家庭购买商品房的人均面积为x平方米,缴纳房款y万元,请求出y关于x的函数关系式;
(3)若该家庭购买商品房的人均面积为50平方米,缴纳房款为y万元,且57<y≤60 时,求m的取值范围.

 沿着x轴的负方向以每秒1个单位的长度平移,设在平移过程中该直线被□ABCD截得的线段长度为m,平移时间为t,m与t的函数图像如图②所示.
沿着x轴的负方向以每秒1个单位的长度平移,设在平移过程中该直线被□ABCD截得的线段长度为m,平移时间为t,m与t的函数图像如图②所示.


 (x>0)的函数图象经过点D,点P是一次函数y=kx+3-3k(k≠0)的图象与该反比例函数图象的一个公共点.
(x>0)的函数图象经过点D,点P是一次函数y=kx+3-3k(k≠0)的图象与该反比例函数图象的一个公共点.
 与
与 轴相交于点A,与
轴相交于点A,与 轴相交于点B.
轴相交于点B.
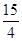 ,试求点P的坐标.
,试求点P的坐标.