题目内容
在半径为1的圆中有一内接多边形,若它的边长皆大于1且小于 ,则这个多边形的边数必为
,则这个多边形的边数必为
- A.7
- B.6
- C.5
- D.4
C
分析:根据圆的半径为1,求出边长均为1时多边形的形状,再求出边长均为 时多边形的形状,则边长皆大于1且小于
时多边形的形状,则边长皆大于1且小于 时多边形的边数处于以上所求两多边形的边数之间.
时多边形的边数处于以上所求两多边形的边数之间.
解答:(1)如图(1),
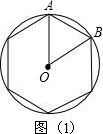
边长均为1时,
△AOB为等边三角形,
故∠AOB=60°,
则这个多边形的边数为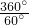 =6边形;
=6边形;
(2)如图,
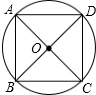
边长均为 时,
时,
在△AOB中,OA=OB=1,AB= ,
,
则AB2=( )2=2,
)2=2,
OA2+OB2=1+1=2,
故AB2=OA2+OB2,
于是△AOB为直角三角形,
则这个多边形的边数为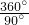 =4边形.
=4边形.
综上,当多边形长皆大于1且小于 时,
时,
这个多边形的边数必为5边形.
故选C.
点评:此题考查了圆内接正多边形边数的判断,利用“夹逼”法,求出边长均为1时多边形的形状和边长均为 时多边形的形状,取其中间值即为正确答案.
时多边形的形状,取其中间值即为正确答案.
分析:根据圆的半径为1,求出边长均为1时多边形的形状,再求出边长均为
 时多边形的形状,则边长皆大于1且小于
时多边形的形状,则边长皆大于1且小于 时多边形的边数处于以上所求两多边形的边数之间.
时多边形的边数处于以上所求两多边形的边数之间.解答:(1)如图(1),

边长均为1时,
△AOB为等边三角形,
故∠AOB=60°,
则这个多边形的边数为
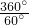 =6边形;
=6边形;(2)如图,

边长均为
 时,
时,在△AOB中,OA=OB=1,AB=
 ,
,则AB2=(
 )2=2,
)2=2,OA2+OB2=1+1=2,
故AB2=OA2+OB2,
于是△AOB为直角三角形,
则这个多边形的边数为
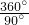 =4边形.
=4边形.综上,当多边形长皆大于1且小于
 时,
时,这个多边形的边数必为5边形.
故选C.
点评:此题考查了圆内接正多边形边数的判断,利用“夹逼”法,求出边长均为1时多边形的形状和边长均为
 时多边形的形状,取其中间值即为正确答案.
时多边形的形状,取其中间值即为正确答案. 
练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
在半径为1的圆中有一内接多边形,若它的边长皆大于1且小于
,则这个多边形的边数必为( )
| 2 |
| A、7 | B、6 | C、5 | D、4 |