题目内容
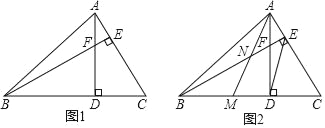
如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.
【答案】(1)BF=AC,理由见解析;(2)NE=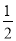 AC,理由见解析.
AC,理由见解析.
【解析】试题分析:(1)如图1,证明△ADC≌△BDF(AAS),可得BF=AC;
(2)如图2,由折叠得:MD=DC,先根据三角形中位线的推论可得:AE=EC,由线段垂直平分线的性质得:AB=BC,则∠ABE=∠CBE,结合(1)得:△BDF≌△ADM,则∠DBF=∠MAD,最后证明∠ANE=∠NAE=45°,得AE=EN,所以EN=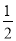 AC.
AC.
试题解析:
(1)BF=AC,理由是:
如图1,∵AD⊥BC,BE⊥AC,
∴∠ADB=∠AEF=90°,
∵∠ABC=45°,
∴△ABD是等腰直角三角形,
∴AD=BD,
∵∠AFE=∠BFD,
∴∠DAC=∠EBC,
在△ADC和△BDF中,
∵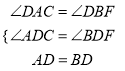 ,
,
∴△ADC≌△BDF(AAS),
∴BF=AC;
(2)NE=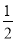 AC,理由是:
AC,理由是:
如图2,由折叠得:MD=DC,
∵DE∥AM,
∴AE=EC,
∵BE⊥AC,
∴AB=BC,
∴∠ABE=∠CBE,
由(1)得:△ADC≌△BDF,
∵△ADC≌△ADM,
∴△BDF≌△ADM,
∴∠DBF=∠MAD,
∵∠DBA=∠BAD=45°,
∴∠DBA﹣∠DBF=∠BAD﹣∠MAD,
即∠ABE=∠BAN,
∵∠ANE=∠ABE+∠BAN=2∠ABE,
∠NAE=2∠NAD=2∠CBE,
∴∠ANE=∠NAE=45°,
∴AE=EN,
∴EN=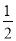 AC.
AC.
【题型】解答题
【结束】
19
某校学生会决定从三明学生会干事中选拔一名干事当学生会主席,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 80 | 90 |
面试 | 93 | 70 | 68 |
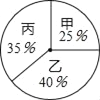
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率如扇形统计图所示(没有弃权,每位同学只能推荐1人),每得1票记1分.
(1)分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按3:3:4的比例确定个人成绩,三人中谁会当选学生会主席?


 过
过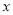 轴上的点A(2,0),且与抛物线
轴上的点A(2,0),且与抛物线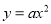 交于B,C两点,点B坐标为(1,1).
交于B,C两点,点B坐标为(1,1). 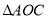 的面积.
的面积.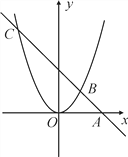
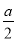 <
<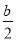 C. 3a-4>3b-4 D. 4-3a>4-3b
C. 3a-4>3b-4 D. 4-3a>4-3b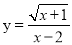 ,自变量
,自变量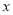 的取值范围是_____.
的取值范围是_____.
 ;(2)
;(2) ;(3)A、①
;(3)A、① ;②
;② ;B、①
;B、① 或
或 ;②
;② 或
或 .
. 可求得答案;(3)A.①由矩形ABEF∽矩形FECD,列出比例式整理可得;②由每个小矩形都是全等的,可得其边长为b和
可求得答案;(3)A.①由矩形ABEF∽矩形FECD,列出比例式整理可得;②由每个小矩形都是全等的,可得其边长为b和 a,列出比例式整理即可;B.①分当FM是矩形DFMN的长时和当DF是矩形DFMN的长时两种情况,根据相似多边形的性质列比例式求解;②由题意可知纵向2块矩形全等,横向3块矩形也全等,所以DN=
a,列出比例式整理即可;B.①分当FM是矩形DFMN的长时和当DF是矩形DFMN的长时两种情况,根据相似多边形的性质列比例式求解;②由题意可知纵向2块矩形全等,横向3块矩形也全等,所以DN= b,然后分当FM是矩形DFMN的长时和当DF是矩形DFMN的长时两种情况,根据相似多边形的性质列比例式求解.
b,然后分当FM是矩形DFMN的长时和当DF是矩形DFMN的长时两种情况,根据相似多边形的性质列比例式求解. AD,
AD, ==
== ;
; =
= ,
, b;
b; a,
a, b;
b; b,
b, a,
a,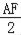 =
= =
= a,
a, b;
b; ,
, ,
,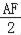 =
= ,
, b;
b; 或
或 ;
; b,
b,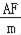 =
= =
= a,
a, b;
b; ,
, ,
, =
= ,
, b;
b; b或
b或

 个单位/秒的速度向终点B匀速运动,当E,F中任意一点到达终点时另一点也随之停止运动,连接EF,设运动时间为t秒,当t为何值时,△AEF为直角三角形?
个单位/秒的速度向终点B匀速运动,当E,F中任意一点到达终点时另一点也随之停止运动,连接EF,设运动时间为t秒,当t为何值时,△AEF为直角三角形?