题目内容
【题目】已知二次函数y=x2-2x-3的图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为D.
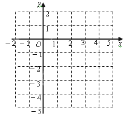
(1)求点A、B、C、D的坐标,并在下面直角坐标系中画出该二次函数的大致图象;
(2)说出抛物线y=x2-2x-3可由抛物线y=x2如何平移得到?
(3)求四边形OCDB的面积.
【答案】A(﹣1,0),B(3,0),C(0,﹣3),D(1,﹣4),图象详见解析;(2)抛物线y=x2-2x-3可由y=x2先向右平移1个单位,再向下平移4个单位而得到;(3)![]() .
.
【解析】
(1)抛物线的解析式中,令x=0,可求出C点的坐标,令y=0,可求出A、B的坐标;将二次函数的解析式化为顶点式,即可得到顶点D的坐标;
(2)将抛物线的解析式化为顶点式,然后再根据“左加右减,上加下减”的平移规律来进行判断;
(3)由于四边形OCDB不规则,可连接OD,将四边形OCDB的面积分成△OCD和△OBD两部分求解.
(1)∵二次函数y=x2﹣2x﹣3可化为y=(x+1)(x﹣3),A在B的左侧,
∴A(﹣1,0),B(3,0),
∵c=﹣3,
∴C(0,﹣3),
∵x=![]() =
=![]() =1,y=
=1,y=![]() =﹣4,
=﹣4,
∴D(1,﹣4),
故此函数的大致图象为:

(2)抛物线y=x2-2x-3可由y=x2先向右平移1个单位,再向下平移4个单位而得到;
(3)连接CD、BD,

则四边形OCDB的面积=S矩形OEFB﹣S△BDF﹣S△CED=OB|OE|﹣![]() DF|BF|﹣
DF|BF|﹣![]() DECE=3×4﹣
DECE=3×4﹣![]() ×2×4﹣
×2×4﹣![]() ×1×1=12﹣4﹣
×1×1=12﹣4﹣![]() =
=![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某通信公司策划了![]() 两种上网的月收费方式:
两种上网的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/ | 超时费/(元/ |
| 30 | 25 | 0.05 |
|
|
|
|
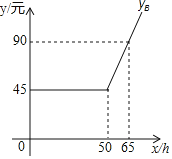
设每月上网时间为![]() ,方式
,方式![]() 的收费金额分别为
的收费金额分别为![]() (元),
(元),![]() (元),如图是
(元),如图是![]() 与
与![]() 之间函数关系的图象.(友情提示:若累计上网时间不超出包时上网时间,则只收月使用费;若累计上网时间超出包时上网时间,则对超出部分再加收超时费)
之间函数关系的图象.(友情提示:若累计上网时间不超出包时上网时间,则只收月使用费;若累计上网时间超出包时上网时间,则对超出部分再加收超时费)
(1)![]() ,
,![]() ,
,![]() ;
;
(2)求![]() 之间的函数解析式;
之间的函数解析式;
(3)若每月上网时间为31小时,请直接写出选择哪种方式能节省上网费.