题目内容
如图所示.从锐角三角形ABC的顶点B向对边作垂线BE.其中AE=3| 3 |
| 3 |
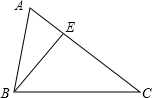
分析:在直角△AEB中,已知AE,AB根据勾股定理可以计算BE的长,在直角△BEC中,已知BE、BC=2CE,根据勾股定理求BC的长度
解答:解:在直角△AEB中,AE=3
,AB=5
,
则BE=
=4
,
∵∠BEC=90°,∠EBC=30°,
∴BC=2CE(直角三角形中30°角所对直角边为斜边长的一半),
∵BC2=CE2+BE2,
∴3CE2=BE2=48,
∴CE=4,BC=8.
答:BC的长为 8.
| 3 |
| 3 |
则BE=
| AB2-AE2 |
| 3 |
∵∠BEC=90°,∠EBC=30°,
∴BC=2CE(直角三角形中30°角所对直角边为斜边长的一半),
∵BC2=CE2+BE2,
∴3CE2=BE2=48,
∴CE=4,BC=8.
答:BC的长为 8.
点评:本题考查了勾股定理的灵活运用,考查了直角三角形中30°角所对直角边为斜边长的一半的定理.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
 7、如图所示,在锐角三角形ABC中,BD,CE分别是AC,AB边上的高,且BD,CE交于点F,若∠A=52°,则∠BFC的度数是( )
7、如图所示,在锐角三角形ABC中,BD,CE分别是AC,AB边上的高,且BD,CE交于点F,若∠A=52°,则∠BFC的度数是( )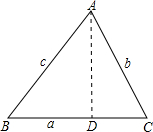 过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明.
过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明. ,AB=5
,AB=5
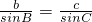
 过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明.
过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明. ,则AD=csinB
,则AD=csinB ,则AD=bsinC
,则AD=bsinC ,∠C=60°,求∠B的度数.
,∠C=60°,求∠B的度数.