题目内容
 如图,D是△ABC的边AB上的一点,过D作DE∥BC交AC于E.已知AD:BD=3:2,则S△ADE:SBCED=________.
如图,D是△ABC的边AB上的一点,过D作DE∥BC交AC于E.已知AD:BD=3:2,则S△ADE:SBCED=________.
9:16
分析:根据相似三角形面积的比等于相似比的平方可求S△ADE:SBCED=9:16.
解答:∵DE∥BC
∴△ADE∽△ABC
∴S△ADE:S△ABC=AD2:AB2=9:25
∴S△ADE:SBCED=9:16.
点评:本题考查了相似三角形的性质:相似三角形面积的比等于相似比的平方.
分析:根据相似三角形面积的比等于相似比的平方可求S△ADE:SBCED=9:16.
解答:∵DE∥BC
∴△ADE∽△ABC
∴S△ADE:S△ABC=AD2:AB2=9:25
∴S△ADE:SBCED=9:16.
点评:本题考查了相似三角形的性质:相似三角形面积的比等于相似比的平方.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
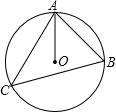 如图,⊙O是△ABC的外接圆,已知∠B=62°,则∠CAO的度数是( )
如图,⊙O是△ABC的外接圆,已知∠B=62°,则∠CAO的度数是( )| A、28° | B、30° | C、31° | D、62° |
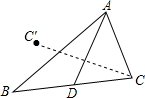 如图,AD是△ABC的中线,∠ADC=60°,点C′与点C关于直线AD对称,若BC=6cm,则点B与点C′之间的距离为
如图,AD是△ABC的中线,∠ADC=60°,点C′与点C关于直线AD对称,若BC=6cm,则点B与点C′之间的距离为 15、如图,AD是△ABC的角平分线,∠B=60°,E,F分别在AC、AB上,且AE=AF,∠CDE=∠BAC,那么,图中长度一定与DE相等的线段共有
15、如图,AD是△ABC的角平分线,∠B=60°,E,F分别在AC、AB上,且AE=AF,∠CDE=∠BAC,那么,图中长度一定与DE相等的线段共有
 如图,⊙O是△ABC的外接圆,AB是直径,若∠B=50°,则∠A等于( )
如图,⊙O是△ABC的外接圆,AB是直径,若∠B=50°,则∠A等于( ) 如图,AD是△ABC的外接圆直径,AD=
如图,AD是△ABC的外接圆直径,AD=