题目内容
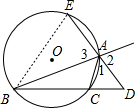如图，已知△ABC内接于⊙O，∠A的外角平分线交BC的延长线于D，交⊙O于E，求证：AD2=BD•CD-AB•AC．考点：正弦定理与余弦定理,圆周角定理,圆内接四边形的性质,相似三角形的判定与性质
专题：证明题
分析：易证△CEA∽△DBA，从而得到AB•AC=AD•AE，易证△DEC∽△DBA，从而得到DE•DA=DB•DC，就可证到结论．
解答：证明：连接EC，如图所示，
根据圆周角定理可得∠CEA=∠CBA．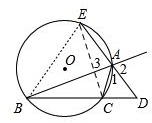
∵∠3=∠2，∠1=∠2，
∴∠3=∠1，
∴∠EAC=∠BAD．
∵∠CEA=∠CBA，∠EAC=∠BAD，
∴△CEA∽△DBA，
∴
=
，
∴AB•AC=AD•AE．
∵∠D=∠D，∠CED=∠ABD，
∴△DEC∽△DBA，
∴
=
，
∴DE•DA=DB•DC，
∴AB•AC=AD•AE=AD•（DE-AD）=AD•DE-AD2，
∴AD2=AD•DE-AB•AC=BD•CD-AB•AC．
根据圆周角定理可得∠CEA=∠CBA．
∵∠3=∠2，∠1=∠2，
∴∠3=∠1，
∴∠EAC=∠BAD．
∵∠CEA=∠CBA，∠EAC=∠BAD，
∴△CEA∽△DBA，
∴
| AC |
| AD |
| AE |
| AB |
∴AB•AC=AD•AE．
∵∠D=∠D，∠CED=∠ABD，
∴△DEC∽△DBA，
∴
| DE |
| DB |
| DC |
| DA |
∴DE•DA=DB•DC，
∴AB•AC=AD•AE=AD•（DE-AD）=AD•DE-AD2，
∴AD2=AD•DE-AB•AC=BD•CD-AB•AC．
点评：本题主要考查圆周角定理、圆的内接四边形的性质、相似三角形的判定与性质等知识，而证得△CEA∽△DBA及△DEC∽△DBA是解决本题的关键．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
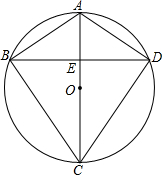如图，AC是⊙O的直径，弦BD垂直平分AO，E为垂足．