题目内容
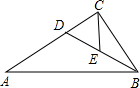 在△ABC中,∠ACB=90°,∠A=30°,BD平分∠ABC交AC于点D,若点E为BD的中点,CE=3,则BE=
在△ABC中,∠ACB=90°,∠A=30°,BD平分∠ABC交AC于点D,若点E为BD的中点,CE=3,则BE=分析:(1)在△DBC中,∠ACB=90°,斜边上的中线等于斜边的一半,所以EC=BE;
(2)∠A=∠ABD=∠CBD=30°,等角对等边,所以AD=BD=2BE.
(2)∠A=∠ABD=∠CBD=30°,等角对等边,所以AD=BD=2BE.
解答:解:(1)在△ABC中,∠ACB=90°,
∴在△DBC中,∠ACB=90°,点E为BD的中点,
∴BE=DE=CE,
∵CE=3,
∴BE=3.
(2)在△ABC中,∠ACB=90°,∠A=30°,BD平分∠ABC,
∴∠ABD=∠CBD=
∠ABC,
∵∠ABC=90°-30°=60°,
∴∠ABD=∠A,
∴AD=BD,
又∵BD=2BE,
∴AD=6.
∴在△DBC中,∠ACB=90°,点E为BD的中点,
∴BE=DE=CE,
∵CE=3,
∴BE=3.
(2)在△ABC中,∠ACB=90°,∠A=30°,BD平分∠ABC,
∴∠ABD=∠CBD=
| 1 |
| 2 |
∵∠ABC=90°-30°=60°,
∴∠ABD=∠A,
∴AD=BD,
又∵BD=2BE,
∴AD=6.
点评:本题考查了直角三角形的性质,在直角三角形中,斜边上的中线等于斜边的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,AC=8,BC=6,AB=10,则△ABC的外接圆半径长为( )
| A、10 | B、5 | C、6 | D、4 |
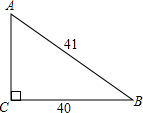 如图,在△ABC中,AC=
如图,在△ABC中,AC= 如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D.
如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D. (2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=
(2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=