题目内容
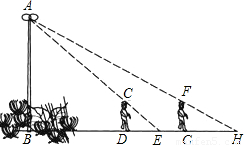
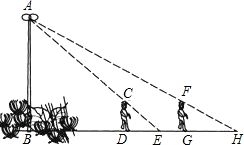如图，花丛中有一路灯杆AB．在灯光下，小明在D点处的影长DE=3米，沿BD方向行走到达G点，DG=5米，这时小明的影长GH=5米．如果小明的身高为1.7米，求路灯杆AB的高度（精确到0.1米）．
分析：根据AB⊥BH，CD⊥BH，FG⊥BH，可得：△ABE∽△CDE，则有
=
和
=
，而
=
，即
=
，从而求出BD的长，再代入前面任意一个等式中，即可求出AB．
| CD |
| AB |
| DE |
| DE+BD |
| FG |
| AB |
| HG |
| HG+GD+BD |
| CD |
| AB |
| FG |
| AB |
| DE |
| DE+BD |
| HG |
| HG+GD+BD |
解答：解：根据题意得：AB⊥BH，CD⊥BH，FG⊥BH，（1分）
在Rt△ABE和Rt△CDE中，
∵AB⊥BH，CD⊥BH，
∴CD∥AB，
可证得：
△ABE∽△CDE，（3分）
∴
=
①，（4分）
同理：
=
②，（5分）
又CD=FG=1.7m，
由①、②可得：
=
，
即
=
，
解之得：BD=7.5m，（6分）
将BD=7.5代入①得：
AB=5.95m≈6.0m．（7分）
答：路灯杆AB的高度约为6.0m．（8分）
（注：不取近似数的，与答一起合计扣1分）
在Rt△ABE和Rt△CDE中，
∵AB⊥BH，CD⊥BH，
∴CD∥AB，
可证得：
△ABE∽△CDE，（3分）
∴
| CD |
| AB |
| DE |
| DE+BD |
同理：
| FG |
| AB |
| HG |
| HG+GD+BD |
又CD=FG=1.7m，
由①、②可得：
| DE |
| DE+BD |
| HG |
| HG+GD+BD |
即
| 3 |
| 3+BD |
| 5 |
| 10+BD |
解之得：BD=7.5m，（6分）
将BD=7.5代入①得：
AB=5.95m≈6.0m．（7分）
答：路灯杆AB的高度约为6.0m．（8分）
（注：不取近似数的，与答一起合计扣1分）
点评：解这道题的关键是将实际问题转化为数学问题，本题只要把实际问题抽象到相似三角形中，利用相似比列出方程即可求出．
练习册系列答案
名校课堂系列答案
相关题目
如图，花丛中有一路灯杆AB．在灯光下，小明在D点处的影长DE=3米，沿BD方向行走到达G点，DG=5米，这时小明的影长GH=5米．如果小明的身高为1.7米，求路灯杆AB的高度是
