题目内容
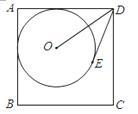
【题目】如图,已知![]() ,垂足为
,垂足为![]() ,将线段
,将线段![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() ,得到线段
,得到线段![]() ,连接
,连接![]() .
.

(1)线段![]() ;
;
(2)求线段![]() 的长度.
的长度.
【答案】(1)4;(2)![]() .
.
【解析】
试题分析:(1)证明△ACD是等边三角形,据此求解;
(2)作DE⊥BC于点E,首先在Rt△CDE中利用三角函数求得DE和CE的长,然后在Rt△BDE中利用勾股定理求解.
试题解析:(1)∵AC=AD,∠CAD=60°,
∴△ACD是等边三角形,
∴DC=AC=4.
(2)作DE⊥BC于点E.

∵△ACD是等边三角形,
∴∠ACD=60°,
又∵AC⊥BC,
∴∠DCE=∠ACB-∠ACD=90°-60°=30°,
∴Rt△CDE中,DE=![]() DC=2,
DC=2,
CE=DCcos30°=4×![]() ,
,
∴BE=BC-CE=3![]() -2
-2![]() =
=![]() .
.
∴Rt△BDE中,BD=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目